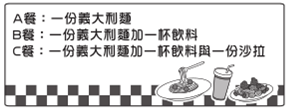
（1）已知一长方形的长为2a,宽为（a+3），将其分割成4个完全一样的直角三角形，如图1所示，再用这4个直角三角形拼成包含大小两个正方形的图形，如图2所示，则图2中小正方形的面积

9

9

；（阴影部分）（2）另一长为2a,宽为2b（a＞b）的长方形，将其分割成8个完全一样的直角三角形，如图3所示，再用这8个直角三角形拼成包含三个正方形的图形，如图4所示．
①用两种不同的方法表示图4中最大的正方形的面积．（用含a,b的代数式表示）
方法1：

（a+b）²

（a+b）²

；方法2：

4ab+（a-b）²

4ab+（a-b）²

．
②根据图中信息求解：
（i）请直接写出（a+b）²，ab,（a-b）²这三个代数式之间的等量关系；
（ii）若图3中长为2a,宽为2b（a＞b）的长方形的周长为24，面积为20，求图4中最小的正方形的边长．