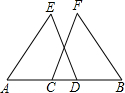
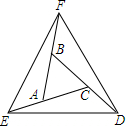
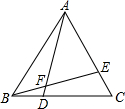
两个等腰三角形△ABC,△ADP,AB=AC,AD=AP,∠DAP=∠BAC,其中P在边BC所在的直线上.连接CD.
问题一:当∠BAC=90°,且点P在线段BC上移动时,则∠BAC,∠BCD之间有怎样的数量关系?请说明理由;
问题二:当0°<∠BAC<180°,且点P还在线段BC上移动,此时∠BAC,∠BCD之间有怎样的数量关系?请说明理由;
随着探究的深入,得出一些基本的结论:当点P在直线BC上移动,所处的位置不同,∠BAC,∠BCD可能的数量关系是什么?(直接写出数量关系即可).

【考点】全等三角形的判定与性质;三角形综合题.
【答案】问题一:∠BAC=∠BCD=90°,理由见解答过程;
问题二:当0°<∠BAC<180°,且点P在线段BC上移动时,∠BCD+∠BAC=180°;理由见解答过程;
探究深入:当点P在线段BC上,或在BC延长线上时,∠BCD+∠BAC=180°;当点P在CB延长线上时,∠BCD=∠BAC.理由见解答过程.
问题二:当0°<∠BAC<180°,且点P在线段BC上移动时,∠BCD+∠BAC=180°;理由见解答过程;
探究深入:当点P在线段BC上,或在BC延长线上时,∠BCD+∠BAC=180°;当点P在CB延长线上时,∠BCD=∠BAC.理由见解答过程.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/30 8:0:9组卷:82引用:1难度:0.5