初中数学试卷真题_初中数学试卷分析

当前位置：章节挑题

请展开查看知识点列表

人教版：八年级上

教材版本: 人教版人教版（2024）北师大版北师大版（2024）华东师大版华东师大版（2024）苏科版苏科版（2024）湘教版湘教版（2024）青岛版青岛版（2024）浙教版浙教版（2024）冀教版冀教版（2024）沪科版沪科版（2024）鲁教五四版鲁教五四版（2024）北京课改版北京课改版（2024）沪教五四版沪教五四版（2024）人教五四版人教五四版（2024）

年级: 七年级上七年级下八年级上八年级下九年级上九年级下

第11章三角形
第12章全等三角形
第13章轴对称
第14章整式的乘法与因式分解
第15章分式

更多>>

原创

更新中

【解题模型】2024-2025学年人教版八下

解题模型因材施教夯实基础稳步提升

浏览次数：4754 更新：2025年06月12日

原创

已完结

《黄金讲练》2024-2025学年人教版八下同步课堂

知识图解新知探究答疑解惑针对训练

浏览次数：5296 更新：2025年06月10日

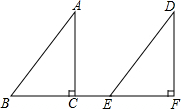2871．如图，点B、C、E、F在同一直线上，BC=EF，AC⊥BC于点C，DF⊥EF于点F，AC=DF．求证：
（1）△ABC≌△DEF；
（2）AB∥DE．
发布：2024/6/27 10:35:59组卷：3088引用：82难度：0.7
解析
2872．观察下列算式：
①1×3-2²=3-4=-1　②2×4-3²=8-9=-1　③3×5-4²=15-16=-1
（1）请你按照三个算式的规律写出第④个、第⑤个算式；
（2）把这个规律用含字母的式子表示出来，并说明其正确性．
发布：2024/6/27 10:35:59组卷：499引用：10难度：0.3
解析
2873．如图，已知△ABC中，AB=AC=10cm,BC=8cm,点D为AB的中点．
（1）如果点P在线段BC上以3cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．
①若点Q的运动速度与点P的运动速度相等，经过1s后，△BPD与△CQP是否全等，请说明理由；
②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？
（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？
发布：2024/6/27 10:35:59组卷：11056引用：145难度：0.1
解析
2874．用简便方法计算：
（1）
（
-
9
）
3
×
（
-
2
3
）
3
×
（
1
3
）
3

（2）-0.25¹⁴×2³⁰
发布：2024/6/27 10:35:59组卷：478引用：6难度：0.5
解析
2875．（1）如图1，△ABC中，∠ABC的平分线与外角∠ACD的平分线相交于P点，请探究∠P与∠A的关系，并说明理由．
（2）如图2、3，四边形ABCD中，设∠A=α，∠D=β，∠P为四边形ABCD的内角∠ABC的平分线与外角∠DCE的平分线所在直线相交而形成的锐角．请利用（1）中的结论完成下列问题：
①如图2，若α+β＞180°，直接写出∠P的度数．（用α，β的代数式表示）
②如图3，若α+β＜180°，直接写出∠P的度数．（用α，β的代数式表示）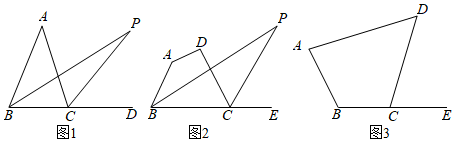
发布：2024/6/27 10:35:59组卷：1190引用：3难度：0.5
解析
2876．已知：如图，AB=AC，DB=DC，
（1）若E、F、G、H分别是各边的中点，求证：EH=FG；
（2）若连接AD、BC交于点P，问AD、BC有何关系？证明你的结论．
发布：2024/6/27 10:35:59组卷：249引用：3难度：0.3
解析
2877．已知a,b,c为实数，且多项式x³+ax²+bx+c能被多项式x²+3x-4整除，
（1）求4a+c的值；
（2）求2a-2b-c的值；
（3）若a,b,c为整数，且c≥a＞1，试确定a,b,c的值．
发布：2024/6/27 10:35:59组卷：6624引用：13难度：0.1
解析
2878．观察下列关于自然数的等式：
（1）3²-4×1²=5
（2）5²-4×2²=9
（3）7²-4×3²=13
…
根据上述规律解决下列问题：
（1）完成第五个等式：11²-4×
²=
；
（2）写出你猜想的第n个等式（用含n的式子表示），并验证其正确性．
发布：2024/6/27 10:35:59组卷：1780引用：16难度：0.5
解析
2879．阅读下列材料：
因式分解的常用方法有提取公因式法和公式法，但有的多项式仅用上述方法就无法分解，如x²-2xy+y²-16．我们细心观察这个式子就会发现，前三项符合完全平方公式，进行变形后可以与第四项结合再运用平方差公式进行分解．
过程如下：
x²-2xy+y²-16
=（x-y）²-16
=（x-y+4）（x-y-4）．
这种因式分解的方法叫分组分解法．
利用这种分组的思想方法解决下列问题：
（1）因式分解：a²-6ab+9b²-25；
（2）因式分解：x²-4y²-2x+4y；
（3）△ABC三边a,b,c满足a²+c²+2b²-2ab-2bc=0，判断△ABC的形状并说明理由．
发布：2024/6/27 10:35:59组卷：1941引用：7难度：0.5
解析
2880．先化简，再求值：（1-
1
a
+
2
）÷
a
2
+
2
a
+
1
a
2
-
4
，其中a=（2021-π）⁰．
发布：2024/6/27 10:35:59组卷：864引用：2难度：0.5
解析

首页上一页 …285 286 287 288 …下一页尾页

2871．如图，点B、C、E、F在同一直线上，BC=EF，AC⊥BC于点C，DF⊥EF于点F，AC=DF．求证：（1）△ABC≌△DEF；（2）AB∥DE．

2872．观察下列算式：①1×3-22=3-4=-1 ②2×4-32=8-9=-1 ③3×5-42=15-16=-1（1）请你按照三个算式的规律写出第④个、第⑤个算式；（2）把这个规律用含字母的式子表示出来，并说明其正确性．

2874．用简便方法计算：（1）（-9）3×（-23）3×（13）3（2）-0.2514×230

2876．已知：如图，AB=AC，DB=DC，（1）若E、F、G、H分别是各边的中点，求证：EH=FG；（2）若连接AD、BC交于点P，问AD、BC有何关系？证明你的结论．

2877．已知a,b,c为实数，且多项式x3+ax2+bx+c能被多项式x2+3x-4整除，（1）求4a+c的值；（2）求2a-2b-c的值；（3）若a,b,c为整数，且c≥a＞1，试确定a,b,c的值．

2878．观察下列关于自然数的等式：（1）32-4×12=5（2）52-4×22=9（3）72-4×32=13…根据上述规律解决下列问题：（1）完成第五个等式：112-4×2=；（2）写出你猜想的第n个等式（用含n的式子表示），并验证其正确性．

2880．先化简，再求值：（1-1a+2）÷a2+2a+1a2-4，其中a=（2021-π）0．

2871．如图，点B、C、E、F在同一直线上，BC=EF，AC⊥BC于点C，DF⊥EF于点F，AC=DF．求证：
（1）△ABC≌△DEF；
（2）AB∥DE．

2872．观察下列算式：
①1×3-2²=3-4=-1　②2×4-3²=8-9=-1　③3×5-4²=15-16=-1
（1）请你按照三个算式的规律写出第④个、第⑤个算式；
（2）把这个规律用含字母的式子表示出来，并说明其正确性．

2874．用简便方法计算：
（1）
（
-
9
）
3
×
（
-
2
3
）
3
×
（
1
3
）
3

（2）-0.25¹⁴×2³⁰

2876．已知：如图，AB=AC，DB=DC，
（1）若E、F、G、H分别是各边的中点，求证：EH=FG；
（2）若连接AD、BC交于点P，问AD、BC有何关系？证明你的结论．

2877．已知a,b,c为实数，且多项式x³+ax²+bx+c能被多项式x²+3x-4整除，
（1）求4a+c的值；
（2）求2a-2b-c的值；
（3）若a,b,c为整数，且c≥a＞1，试确定a,b,c的值．

2878．观察下列关于自然数的等式：
（1）3²-4×1²=5
（2）5²-4×2²=9
（3）7²-4×3²=13
…
根据上述规律解决下列问题：
（1）完成第五个等式：11²-4×
²=
；
（2）写出你猜想的第n个等式（用含n的式子表示），并验证其正确性．

2880．先化简，再求值：（1-
1
a
+
2
）÷
a
2
+
2
a
+
1
a
2
-
4
，其中a=（2021-π）⁰．