当前位置：
章节挑题
请展开查看知识点列表
>
更多>>
|
原创
已完结
|
知识图解
新知探究
答疑解惑
针对训练
浏览次数：4710
更新：2025年06月09日
|
|
原创
已完结
|
知识图解
新知探究
答疑解惑
针对训练
浏览次数：7020
更新：2025年06月09日
|
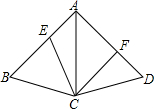2921．如图，四边形ABCD中，AC为∠BAD的角平分线，AB=AD，E、F两点分别在AB、AD上，且AE=DF．请完整说明为何四边形AECF的面积为四边形ABCD的一半．发布：2024/6/27 10:35:59组卷：3253引用：63难度：0.5
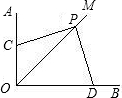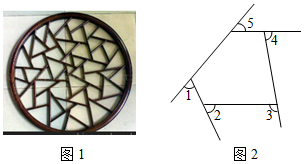
2922．如图，∠AOB=90°，OM平分∠AOB，将直角三角板的顶点P在射线OM上移动，两直角边分别与OA、OB相交于点C、D，问PC与PD相等吗？试说明理由．发布：2024/6/27 10:35:59组卷：7278引用：19难度：0.32923．图1是我国古代建筑中的一种窗格，其中冰裂纹图案象征着坚冰出现裂纹并开始消融，形状无一定规则，代表一种自然和谐美．图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形，则∠1+∠2+∠3+∠4+∠5=度．
发布：2024/6/27 10:35:59组卷：219引用：3难度：0.92924．如图1，已知线段AB，CD相交于点O，连接AD，CB，我们把形如图1的图形称之为“8字形”．如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD，AB分别相交于点M，N，试解答下列问题：
（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系；
（2）在图2中，若∠D=40°，∠B=36°，试求∠P的度数；
（3）如果图2中∠D和∠B为任意角时，其他条件不变，试问∠P与∠D、∠B之间存在着怎样的数量关系（直接写出结论即可）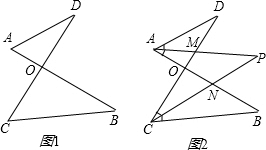
发布：2024/6/27 10:35:59组卷：2416引用：7难度：0.1
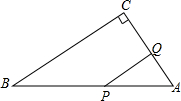2925．如图，在Rt△ABC中，∠C=90°，∠A=60°，AB=12cm,若点P从点B出发以2cm/s的速度向点A运动，点Q从点A出发以1cm/s的速度向点C运动，设P、Q分别从点B、A同时出发，运动的时间为ts.
（1）用含t的式子表示线段AP、AQ的长；
（2）当t为何值时，△APQ是以PQ为底边的等腰三角形？
（3）当t为何值时，PQ∥BC？发布：2024/6/27 10:35:59组卷：2644引用：5难度：0.3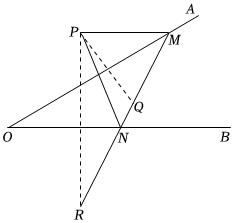
2926．如图，点P是∠AOB外一点，点M、N分别是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在线段MN的延长线上．若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为多少．发布：2024/6/27 10:35:59组卷：940引用：21难度：0.62927．在计算（x+a）（x+b）时，甲把b错看成了6，得到结果是：x2+8x+12；乙错把a看成了-a,得到结果：x2+x-6．
（1）求出a,b的值；
（2）在（1）的条件下，计算（x+a）（x+b）的结果．发布：2024/6/27 10:35:59组卷：2573引用：21难度：0.72928．在△ABC中，∠C=90°，AC＞BC，D是AB的中点．E为直线AC上一动点，连接DE．过点D作DF⊥DE，交直线BC于点F，连接EF．
（1）如图1，当E是线段AC的中点时，设AE=a,BF=b,求EF的长（用含a,b的式子表示）；
（2）当点E在线段CA的延长线上时，依题意补全图2，用等式表示线段AE，EF，BF之间的数量关系，并证明．
发布：2024/6/27 10:35:59组卷：6572引用：21难度：0.52929．阅读某同学对多项式（x2-4x+2）（x2-4x+6）+4进行因式分解的过程，并解决问题：
解：设x2-4x=y,
原式=（y+2）（y+6）+4（第一步）
=y2+8y+16（第二步）
=（y+4）2（第三步）
=（x2-4x+4）2（第四步）
（1）该同学第二步到第三步的变形运用了（填序号）；
A．提公因式法 B．平方差公式
C．两数和的平方公式 D．两数差的平方公式
（2）该同学在第三步用所设的代数式进行了代换，得到第四步的结果，这个结果能否进一步因式分解？（填“能”或“不能”）．如果能，直接写出最后结果．
（3）请你模仿以上方法尝试对多项式（x2+6x）（x2+6x+18）+81进行因式分行解．发布：2024/6/27 10:35:59组卷：1007引用：11难度：0.72930．如图，已知△ABC中，∠ABC和∠ACB的平分线BD、CE相交于点O，且∠A=60°，求∠BOC的度数．
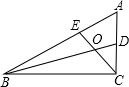发布：2024/6/27 10:35:59组卷：254引用：7难度：0.3
