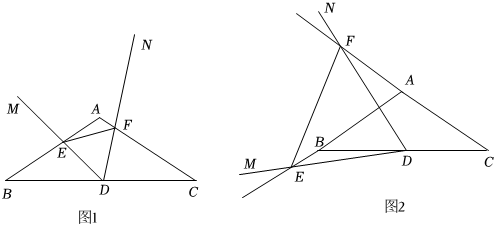
如图，△ABC中，∠BAC=120°，AB=AC，点D是BC中点，∠MDN=60°，∠MDN的两边DM，DN分别与直线AB，AC交于点E，F，DE=DF，连接EF．
（1）如图1，当点E，F分别在AB，AC上时，猜想△DEF形状是 等边等边三角形；线段AE、AF、AB的数量关系是 ABAB．
（2）如图2，当点E，F分别在AB，CA延长线上时，上述两个结论成立吗？若成立，请完成证明；若不成立，请说明理由．
（3）在（2）的条件下，AB=6．
①连接AD，直接写出S△AED-S△AFD=934934．
②当EB=BD时，求AF的长．
9
3
4
9
3
4
【考点】三角形综合题．
【答案】等边；AB；
9
3
4
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/14 8:0:9组卷：429引用：1难度：0.3
相似题
-
1．如图1，△ABC和△CDE都是等边三角形，且A，C，E在同一条直线上，分别连接AD，BE．
（1）求证：AD=BE；
（2）如图2，连接BD，若M，N，Q分别为AB，DE，BD的中点，过N作NP⊥MN与MQ的延长线交于P，求证：MP=AD；
（3）如图3，设AD与BE交于F点，点M在AB上，MG∥AD，交BE于H，交CF的延长线于G，试判断△FGH的形状．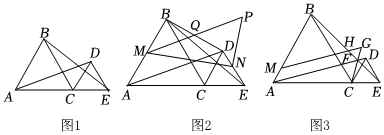
发布：2025/5/24 17:0:2组卷：45引用：1难度：0.1 -
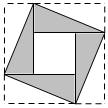2．仔细阅读以下内容解决问题：第24届国际数学家大会会标，设两条直角边的边长为a,b,则面积为ab,四个直角三角形面积和小于正方形的面积得：a2+b2≥2ab,当且仅当a=b时取等号．在a2+b2≥2ab中，若a＞0，b＞0，用12、a代替a,b得，a+b≥2b，即ab（*），我们把（*）式称为基本不等式．利用基本不等式我们可以求这个式子的最大最小值．我们以“已知x为实数，求y=a+b2≥ab的最小值”为例给同学们介绍．x2+4x2+1
解：由题知y=，x2+1+3x2+1=x2+1+3x2+1
∴＞0，x2+1＞0，3x2+1
∴y=，当且仅当x2+1+3x2+1≥2x2+1⋅3x2+1=23时取等号，即当x=x2+1=3x2+1时，函数的最小值为22．3
总结：利用基本不等式（a＞0，b＞0）求最值，若ab为定值．则a+b有最小值．a+b2≥ab
请同学们根据以上所学的知识求下列函数的最值，并求出取得最值时相应x的取值．
（1）若x＞0，求y=2x+的最小值；2x
（2）若x＞2，求y=x+的最小值；1x-2
（3）若x≥0，求y=的最小值．x+4x+13x+2发布：2025/5/24 19:30:1组卷：236引用：3难度：0.5 -
3．（1）如图1，Rt△ABC中，∠C=90°，AB=10，AC=8，E是AC上一点，AE=5，ED⊥AB，垂足为D，求AD的长．
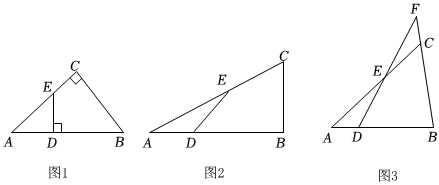
（2）类比探究：如图2，△ABC中，AC=14，BC=6，点D，E分别在线段AB，AC上，∠EDB=∠ACB=60°，DE=2．求AD的长．
（3）拓展延伸：如图3，△ABC中，点D，点E分别在线段AB，AC上，∠EDB=∠ACB=60°．延长DE，BC交于点F，AD=4，DE=5，EF=6，DE＜BD，=；BD=．BCAC发布：2025/5/24 16:30:1组卷：1046引用：6难度：0.1
