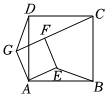
正方形ABCD与正方形AEFG公共一个顶点A，连接BE，CF，DG，AB=4，AE=2，当正方形AEFG绕点A旋转的过程中．
（1）直接写出BE与DG的关系是 BE=DG，BE⊥DGBE=DG，BE⊥DG；
（2）①猜想CFBE的值并证明你的结论：CFBE=2CFBE=2；
②当C，F，G三点在一条直线上时，直接写出BE=14-214-2．
CF
BE
CF
BE
2
CF
BE
2
14
2
14
2
【考点】相似形综合题．
【答案】BE=DG，BE⊥DG；=；-
CF
BE
2
14
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/21 12:0:1组卷：9引用：1难度：0.3
相似题
-
1．问题背景 如图（1），已知△ABC∽△ADE，求证：△ABD∽△ACE；
尝试应用 如图（2），在△ABC和△ADE中，∠BAC=∠DAE=90°，∠ABC=∠ADE=30°，AC与DE相交于点F，点D在BC边上，=ADBD，求3的值；DFCF
拓展创新 如图（3），D是△ABC内一点，∠BAD=∠CBD=30°，∠BDC=90°，AB=4，AC=2，直接写出AD的长．3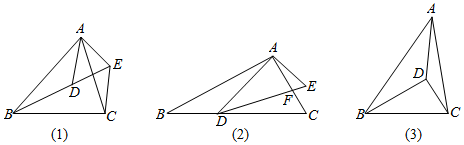
发布：2025/5/23 7:0:1组卷：11448引用：43难度：0.7 -
2．如图1，在正方形ABCD中，点E、F分别在BC、CD上，且BE=DF，AE、AF分别与BD交于点G、H，过点G作GN⊥AF，垂足为M，交AD于点N．
（1）求证：AH=GN；
（2）若∠EAF=45°，求证：；AHAF=BGCF
（3）如图2，过点G作GQ⊥AD，垂足为Q，交AF于点P．若GM=4MN，求的值．APGP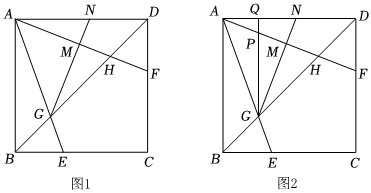
发布：2025/5/23 7:0:1组卷：331引用：2难度：0.1 -
3．【初步尝试】
（1）如图1，在正方形ABCD中，点E，F分别为AB、AD边上的点且DE⊥CF，求证：DE=CF．
（2）【思考探究】
如图2，在矩形ABCD中，AB=3，BC=2，点E为BC中点，点F为AE上一点，连接CF、DF且CF=CD，求DF的值．
（3）【拓展应用】
如图3，在四边形ABCD中，∠DAB=90°，∠ABC=45°，，点E、F分别在线段AB、AD上，且CE⊥BF．直接写出BC=23AB的值．CEBF
发布：2025/5/23 7:0:1组卷：409引用：1难度：0.1
