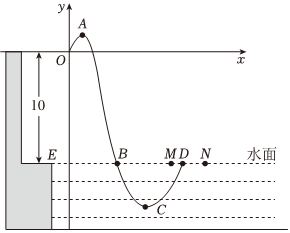
如图，某跳水运动员在10米跳台上进行跳水训练，水面边缘点E的坐标为（-1，-10），运动员（将运动员看成一点）在空中运动的路线是经过原点O的抛物线．在跳某个规定动作时，运动员在空中最高处A点的坐标为（34，916），正常情况下，运动员在距水面高度5米之前，必须完成规定的翻腾、打开动作，并调整好入水姿势，否则就会失误，运动员入水后，运动路线为另一条抛物线．
（1）求运动员在空中运动时对应抛物线的解析式，并求出入水处点B的坐标．
（2）若运动员在空中调整好入水姿势时，恰好距点E的水平距离为4米，问该运动员此次跳水会不会失误？通过计算说明理由．
（3）在该运动员入水点的正前方有M，N两点，且EM=7，EN=9，该运动员入水后运动路线对应的抛物线解析式为y=（x-h）2+k,若该运动员出水点D在MN之间（包括M，N两点），则k的取值范围是 -14≤k≤-11-14≤k≤-11．
（
3
4
，
9
16
）
【考点】二次函数的应用．
【答案】-14≤k≤-11
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/12 3:0:1组卷：838引用：3难度：0.3
相似题
-
1．第二十四届冬奥会在北京成功举办，在跳台滑雪项目中，运动员首先沿着跳台助滑道飞速下滑，然后在起跳点腾空，身体在空中飞行至着陆坡着陆，再滑行到停止区终止．某数学小组对该项目中的数学问题进行了深入研究，如图是该小组绘制的赛道截面图，以停止区CD所在水平线为x轴，过起跳点A与x轴垂直的直线为y轴，O为坐标原点，建立平面直角坐标系，AC为着陆坡，OA=65m,某运动员在A处起跳腾空后，飞行至着陆坡的B处着陆，过点B作BE⊥y轴于点E，且BE=50
m,在空中飞行过程中，运动员到x轴的距离y（m）与水平方向移动的距离x（m）具备二次函数关系，其解析式为y=-3x+c.160x2+32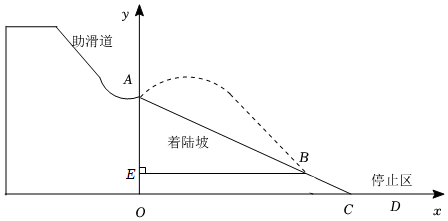
（1）c=，点B的坐标为 ；
（2）进一步研究发现，该运动员在飞行过程中，其水平方向移动的距离x（m）与飞行时间t（s）具备一次函数关系，当运动员在起跳点腾空时，t=0，x=0；空中飞行5s后着陆．
①求x关于t的函数解析式；
②当t为何值时，运动员离着陆坡的竖直距离h最大，最大值是多少？发布：2025/6/14 20:30:2组卷：125引用：1难度：0.6 -
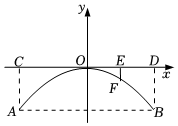2．如图是一座抛物线形拱桥侧面示意图，水面宽AB与桥长CD均为36m,桥拱顶部O离水面的距离为6m,以桥拱顶点O为原点，桥面为x轴建立平面直角坐标系．
OD的中点E到桥拱的距离EF为 m.发布：2025/6/14 20:30:2组卷：122引用：4难度：0.6 -
3．飞机着陆后滑行的距离y关于滑行时间t的函数解析式是
，则飞机着陆滑行所用时间最长为（ ）s.y=60t-32t2发布：2025/6/14 21:0:1组卷：118引用：1难度：0.7
