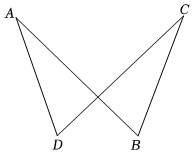
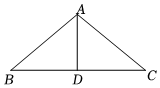
如图，△ABC是等腰直角三角形，∠ACB=90°，AC=BC，在平面内取一点D连接AD、BD，点O为线段AD的中点，连接CO并延长到点F，使OF=CO．以BD为直角边，顺时针方向作等腰Rt△DEB，DB=EB，∠DBE=90°，连DE，CE，BF．

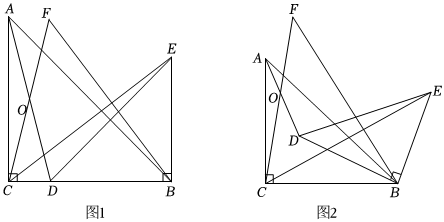
（1）如图1，当D在BC边上时，请直接写出CE与BF的位置和数量关系
CE=BF，CE⊥BF
CE=BF，CE⊥BF
；
（2）如图2，当D在△ABC的内部时，其他条件不变，（1）中的结论是否成立？若成立，请给予证明；若不成立，请说明理由；

【答案】CE=BF，CE⊥BF

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/6/2 8:0:8组卷：657引用：1难度：0.2

相似题

1．已知：如图所示，AB=CD，AD=CB，求证：∠A=∠C．
发布：2025/6/20 4:30:2组卷：80引用：2难度：0.5
解析
2．如图，在△ABC中，AB=AC，AD是BC边上的中线．
（1）△ABD与△ACD全等吗？为什么？
（2）AD⊥BC吗？为什么？
发布：2025/6/20 4:30:2组卷：24引用：1难度：0.6
解析
3．在△ABC中，AB=3cm,AC=4cm,则BC边上的中线AD的取值范围是
．
发布：2025/6/20 4:30:2组卷：149引用：3难度：0.5
解析

1．已知：如图所示，AB=CD，AD=CB，求证：∠A=∠C．