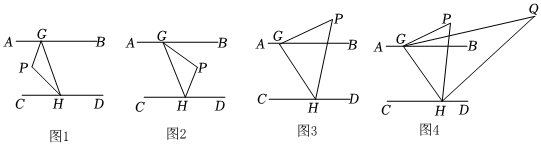
（1）探究：如图1，AB∥CD，点G、H分别在直线AB、CD上，连结PG、PH，当点P在直线GH的左侧时，试说明∠GPH=∠AGP+∠CHP；
（2）变式：如图2，将点P移动到直线GH的右侧，其他条件不变，试探究∠GPH、∠AGP、∠CHP之间的关系，并说明理由；
（3）（问题迁移）如图3，AB∥CD，点P在AB的上方，问∠GPH、∠AGP、∠CHP之间有何数量关系？请说明理由；
（4）（联想拓展）如图4所示，在（2）的条件下，已知∠GPH=α，∠PGB的平分线和∠PHD的平分线交于点Q，用含有α的式子表示∠GQH的度数．
【考点】平行线的判定与性质．
【答案】（1）证明见解答；
（2）∠AGP+∠GPH+∠CHP=360°，理由见解答；
（3）∠GPH=∠AGP-∠CHP，理由见解答；
（4）∠GQH=α．
（2）∠AGP+∠GPH+∠CHP=360°，理由见解答；
（3）∠GPH=∠AGP-∠CHP，理由见解答；
（4）∠GQH=
1
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/29 8:0:10组卷：3408引用：4难度：0.4
相似题
-
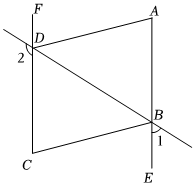1．如图：已知∠1+∠2=180°，∠A=∠C，BC平分∠DBE．
（1）AE与FC平行吗？说明理由．
（2）AD与BC的位置关系如何？为什么？
（3）DA平分∠BDF吗？为什么？发布：2025/5/24 21:0:1组卷：860引用：4难度：0.4 -
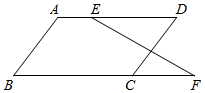2．如图，AB∥CD，∠B=∠D，直线EF与AD，BC的延长线分别交于点E，F，求证：∠DEF=∠F．发布：2025/5/24 8:30:1组卷：2925引用：34难度：0.7 -
3．【数学抽象】实验证明：平面镜反射光线的规律是射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等，如图①，一束光线m射到平面镜a上，被a反射后的光线为n,则入射光线m,反射光线n与平面镜a所夹的锐角相等，即∠1=∠2．
（1）利用这个规律人们制作了潜望镜，图②是潜望镜工作原理示意图，AB、CD是平行放置的两面平面镜，请解释进入潜望镜的光线m为什么和离开潜望镜的光线n是平行的？
（2）如图③，改变两平面镜之间的位置关系，经过两次反射后，入射光线m与反射光线n之间的位置关系会随之改变．若入射光线m与反射光线n平行但方向相反，则两平面镜的夹角∠ABC为多少度？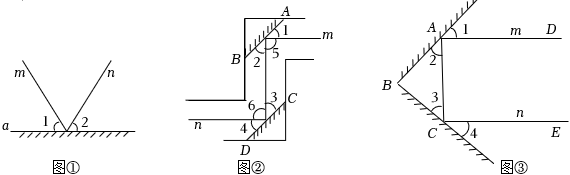
发布：2025/5/24 14:30:1组卷：194引用：3难度：0.8
