△ABC中，AC=BC，∠ACB=90°，D为△ABC外一点．
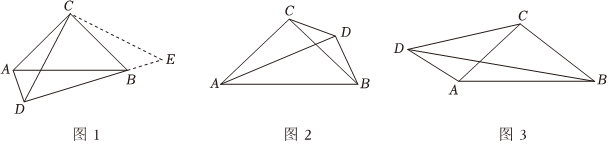
【探究发现】（1）如图1，点D在边AB下方，∠ADB=90°．学校的数学兴趣小组的同学们尝试探究此时线段AD、BD、CD之间的数量关系．他们的思路是这样的，作EC⊥CD，取EC=CD，连接BE．易证△ADC≌△BEC．通过等量代换得到线段之间的数量关系．请根据同学们的思路，写出△ADC≌△BEC的证明过程．
【迁移运用】（2）如图2，点D在边AB上方，∠ADB=90°．猜想线段AD、BD、BC之间的数量关系，并证明你的结论．
【延伸拓展】（3）如图3，在四边形ABCD中，∠ABC=∠BAC=∠ADC=45°，若AD=2，CD=4，请直接写出BD的值．
【考点】四边形综合题．
【答案】（1）证明见解析过程；
（2）BD2+CD2=2AD2，证明见解析过程；
（3）BD=6．
（2）BD2+CD2=2AD2，证明见解析过程；
（3）BD=6．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/4 6:0:3组卷：478引用：2难度：0.5
相似题
-
1．小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．
（1）温故：如图1，在△ABC中，AD⊥BC于点D，正方形PQMN的边QM在BC上，顶点P，N分别在AB，AC上，若BC=6，AD=4，求正方形PQMN的边长．
（2）操作：能画出这类正方形吗？小波按数学家波利亚在《怎样解题》中的方法进行操作：如图2，任意画△ABC，在AB上任取一点P'，画正方形P'Q'M'N'，使Q'，M'在BC边上，N'在△ABC内，连接BN'并延长交AC于点N，画NM⊥BC于点M，NP⊥NM交AB于点P，PQ⊥BC于点Q，得到四边形PQMN．小波把线段BN称为“波利亚线”．
（3）推理：证明图2中的四边形PQMN是正方形．
（4）拓展：在（2）的条件下，在射线BN上截取NE=NM，连接EQ，EM（如图3）．当tan∠NBM=时，猜想∠QEM的度数，并尝试证明．34
请帮助小波解决“温故”、“推理”、“拓展”中的问题．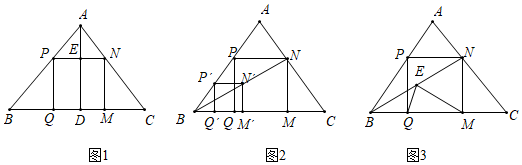
发布：2025/9/11 15:30:1组卷：1910引用：9难度：0.1 -
2．如图，在四边形ABCD中，AB∥CD，∠ABC=∠BCD=90°，AD=10cm,BC=8cm,CD=16cm.点P从点A出发，以每秒3cm的速度沿折线段AB-BC-CD运动，点Q从点D出发，以每秒2cm的速度沿线段DC方向向点C运动．已知动点P、Q同时出发，设运动时间为t秒（0≤t≤8）．
（1）求AB的长；
（2）当四边形PBQD为平行四边形时，求四边形PBQD的周长；
（3）在点P运动过程中，当t=秒的时候，使得△BPQ的面积为20cm2．发布：2025/9/11 15:30:1组卷：615引用：5难度：0.1 -
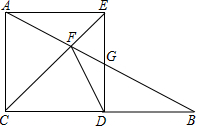3．在Rt△ABC中，∠ACB=90°，AC=12．点D在线段CB上，以CA，CD为边作正方形ACDE，AB与CE，DE的交点分别为F，G．
（1）求证：∠FAE=∠FDE；
（2）若点G为DE的中点，求FG的长．
（3）当△DFG为等腰三角形时，求DG的长．发布：2025/9/11 17:0:1组卷：440引用：3难度：0.3
