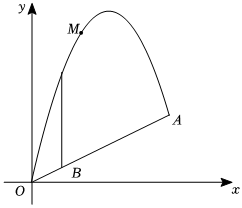
如图，小球M从斜坡OA上的O点处抛出，建立如图所示的平面直角坐标系，球的抛出路线是抛物线L1：y=-12x2+bx的一部分，斜坡可以看作直线L2：y=12x的一部分．若小球经过点（6，6），解答下列问题：
（1）小球在斜坡上的落点为A，求A点的坐标；
（2）在斜坡OA上的B点有一棵树，B点的横坐标为2，树高为4，小球M能否飞过这棵树？通过计算说明理由；
（3）直接写出小球M在飞行的过程中离斜坡OA的最大铅垂高度．
1
2
1
2
【考点】二次函数的应用．
【答案】（1）（7，）；
（2）小球M能飞过这棵树；
理由见解答；
（3）．
7
2
（2）小球M能飞过这棵树；
理由见解答；
（3）
49
8
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/12 7:0:1组卷：67引用：1难度：0.4
相似题
-
1．为了响应政府提出的由中国制造向中国创造转型的号召，某公司自主设计了一款成本为40元的可控温杯，并投放市场进行试销售，经过调查发现该产品每天的销售量y（件）与销售单价x（元）满足一次函数关系：y=-10x+1200．
（1）求出利润S（元）与销售单价x（元）之间的关系式（利润=销售额-成本）；
（2）当销售单价定为多少时，该公司每天获取的利润最大？最大利润是多少元？发布：2025/6/19 8:30:1组卷：3517引用：79难度：0.5 -
2．小明开了一家网店，进行社会实践，计划经销甲、乙两种商品．若甲商品每件利润10元，乙商品每件利润20元，则每周能卖出甲商品40件，乙商品20件．经调查，甲、乙两种商品零售单价分别每降价1元，这两种商品每周可各多销售10件．为了提高销售量，小明决定把甲、乙两种商品的零售单价都降价x元．
（1）直接写出甲、乙两种商品每周的销售量y（件）与降价x（元）之间的函数关系式：y甲=，y乙=；
（2）求出小明每周销售甲、乙两种商品获得的总利润W（元）与降价x（元）之间的函数关系式？如果每周甲商品的销售量不低于乙商品的销售量的，那么当x定为多少元时，才能使小明每周销售甲、乙两种商品获得的总利润最大？32发布：2025/6/19 9:0:1组卷：4425引用：56难度：0.3 -
3．某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．
（1）求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式；
（2）求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？
（3）如果该企业要使每天的销售利润不低于4000元，且每天的总成本不超过7000元，那么销售单价应控制在什么范围内？（每天的总成本=每件的成本×每天的销售量）发布：2025/6/19 8:30:1组卷：8430引用：110难度：0.3
