阅读下列材料，并按要求解答．
【模型介绍】
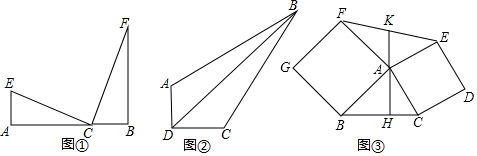
如图①，C是线段A、B上一点E、F在AB同侧，且∠A=∠B=∠ECF=90°，看上去像一个“K“，我们称图①为“K”型图．
【性质探究】
性质1：如图①，若EC=FC，△ACE≌△BFC
性质2：如图①，若EC≠FC，△ACE∽△BFC且相似比不为1．
【模型应用】
应用1：如图②，在四边形ABCD中，∠ADC=90°，AD=1，CD=2，BC=25，AB=5．求BD．
应用2：如图③，已知△ABC，分别以AB、AC为边向外作正方形ABGF、正方形ACDE，AH⊥BC，连接EF．交AH的反向延长线于点K，证明：K为EF中点．
（1）请你完成性质1的证明过程；
（2）请分别解答应用1，应用2提出的问题．
5
【考点】相似形综合题．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/16 3:0:1组卷：475引用：3难度：0.1
相似题
-
1．如图1，在△ABC中，AB=AC=5，BC=8，∠PDQ的顶点D在BC上，DQ经过点A，DP交AB于点E，且BD=3，∠PDQ=∠B．
（1）BE的长是 ；
（2）如图2，把∠PDQ绕顶点D按逆时针方向旋转，在旋转过程中始终保持∠PDQ的开口在BC的上方，且DP不与DB重合，DQ交AB于点G，交CA的延长线于点F（点F不与点A重合），设BE=x,AG=y.
①请说明△BDE与△CFD相似；
②请直接写出y与x的函数关系式，并写出自变量x的取值范围；
③是否存在以∠GFA或∠FGA为顶角的等腰△AGF？若存在，请求出BE的长；若不存在，请说明理由．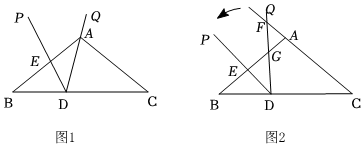
发布：2025/5/26 4:0:1组卷：202引用：1难度：0.2 -
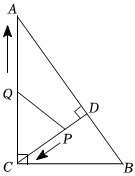2．如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD⊥AB于点D，点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到点C时，两点都停止运动，设运动时间为t秒．
（1）求线段CD的长；
（2）设△CPQ的面积为S，求S与t之间的函数关系式，并写出自变量的取值范围；
（3）当t为何值时，△CPQ与△CAD相似？请直接写出t的值．发布：2025/5/26 3:0:2组卷：983引用：5难度：0.3 -
3．如图，已知平行四边形ABCD中，
，AB=5，tanA=2，点E是射线AD上一动点，过点E作EF⊥AD，垂足为点E，交射线AB于点F，交射线CB于点G，联结CE、CF．设AE=m.AD=5
（1）如图，当点E在边AD上时．
①求证：△AEF∽△BGF．
②当S△DCE=4S△BFG时，求AE：ED的值．
（2）当点E在边AD的延长线上时，是否存在这样的点E使△AEF与△CFG相似？如果存在求出此时AE的长度．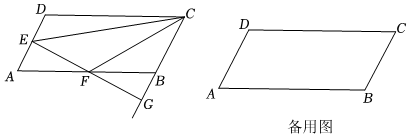
发布：2025/5/26 2:0:6组卷：86引用：1难度：0.2
