党的二十大即将召开，各行各业的人们用拼搏奋斗凝聚起奋进新征程、建功新时代的磅礴力量，信心满怀向未来．某商店决定对某类商品进行降价促销活动．已知进价为每件6元，平时以单价12元的价格售出一天可卖80件．根据调查单价每降低1元，每天可多售出40件；设商品售价x元（售价不低于进价，x为正整数），这批商品的日利润为y元（利润=售价-成本），请解决以下问题：
（1）当商品的售价x为多少元时，销售这批商品的日利润最大，最大值为多少？
（2）当日利润达到280元时，求x的值．
（3）若商店每卖一件就捐m元（m＞0）给希望小学，该店发现售价为11元时可获得最大日利润，求m的取值范围．
【答案】（1）当商品的售价x为19元时，销售这批商品的日利润最大，最大值为640元；
（2）当日利润达到280元时x=7；
（3）m的取值范围为1＜m＜3．
（2）当日利润达到280元时x=7；
（3）m的取值范围为1＜m＜3．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：287引用：3难度：0.4
相似题
-
1．小明同学利用寒假30天时间贩卖草莓，了解到某品种草莓成本为10元/千克，在第x天的销售量与销售单价如下（每天内单价和销售量保持一致）：
设第x天的利润w元．销售量m（千克） m=40-x 销售单价n（元/千克） 当1≤x≤15时，n=20+ x12当16≤x≤30时，n=10+ 300x
（1）请计算第几天该品种草莓的销售单价为25元/千克？
（2）这30天中，该同学第几天获得的利润最大？最大利润是多少？注：利润=（售价-成本）×销售量
（3）在实际销售的前15天中，草莓生产基地为刺激销售，鼓励销售商批发草莓，每批发1千克就发给a（a≥2）元奖励．通过销售记录发现，前8天中，每天获得奖励后的利润随时间x（天）的增大而增大，试求a的取值范围．12发布：2025/6/18 3:0:1组卷：593引用：2难度：0.5 -
2．心理学家发现：学生对提出概念的接受能力y与提出概念的时间x（min）之间满足二次函数关系y=-0.1x2+2.6x+43．则使学生对概念的接受能力最大．则提出概念的时间应为（ ）
发布：2025/6/18 3:30:2组卷：139引用：2难度：0.8 -
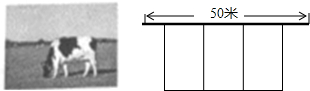3．某农场拟建三间长方形种牛饲养室，饲养室的一面靠墙（墙长50m），中间用两道墙隔开（如图）．已知计划中的建筑材料可建墙的总长度为48m,则这三间长方形种牛饲养室的总占地面积的最大值为 m2．发布：2025/6/18 2:0:1组卷：4327引用：11难度：0.5
