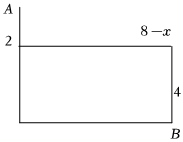
（1）问题再现：学习二次根式时，老师给同学们提出了一个求代数式最小值的问题，如，“求代数式
x
2
+
4
+
（
8
-
x
）
2
+
16
的最小值”．小强同学发现
x
2
+
4
可看作两直角边分别为x和2的直角三角形斜边长，
（
8
-
x
）
2
+
16
可看作两直角边分别是8-x和4的直角三角形的斜边长．于是构造出如图所示，将问题转化为求线段AB的长，进而求得
x
2
+
4
+
（
8
-
x
）
2
+
16
的最小值是
10
10
；
（2）类比迁移：已知a,b均为正数，且a+b=12．求
a
2
+
4
+
b
2
+
9
的最小值；
（3）方法应用：已知a,b均为正数，且
4
a
2
+
b
2
，
a
2
+
b
2
，
a
2
+
4
b
2
是三角形的三边长，求这个三角形的面积（用含a,b的代数式表示）．

【答案】10

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/9/14 10:0:8组卷：225引用：6难度：0.5

相似题

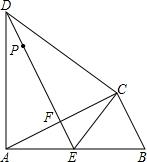1．如图，△ABC中，∠ACB=90°，以AC为底边作等腰三角形△ADC，AD=CD，过点D作DE⊥AC，垂足为F，DE与AB相交于点E，连接CE．AB=5，AC=4，BC=3．
（1）求证：AE=CE=BE；
（2）若P是射线DE上的一点．则当P在何处时，△PBC的周长最小，并求出此时△PBC的周长．
发布：2025/6/25 7:0:2组卷：99引用：1难度：0.3
解析
2．直线MN和同侧两点AB，在MN上找一点P，使得PA+PB最小．（尺规作图）
发布：2025/6/24 17:30:1组卷：114引用：2难度：0.5
解析
3．如图，矩形ABCD中，BC=10，∠BAC=30°，若在AC、AB上各取一点M、N，使BM+MN的值最小，求这个最小值

．
发布：2025/6/24 15:30:2组卷：818引用：2难度：0.5
解析

2．直线MN和同侧两点AB，在MN上找一点P，使得PA+PB最小．（尺规作图）