如图，三角形ABC中，点G在线段BC上，且FG⊥BC交AB于点F．点P在直线AB上运动，PD⊥BC交直线BC于D，过点D作DE∥PA，交直线AC于E．
（1）如图1，当点P在线段AB的延长线上时，求证：∠BFG+∠PDE=180°；
（2）如图2，延长ED至点S，延长BD至点T，当点P在线段BA的延长线上时，点H在线段AC上，连接GH，已知∠FGH+∠PDE=180°，
①求证：GH∥DE；
②若∠PDS：∠SDT=2：3，13∠GFA+∠BAC=120°，求∠GHC的度数．
1
3
【考点】平行线的判定与性质．
【答案】（1）见解答；
（2）①见解答；②72°．
（2）①见解答；②72°．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/28 8:0:9组卷：93引用：3难度：0.6
相似题
-
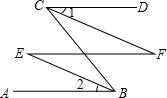1．如图，若∠1=∠2，AB∥CD，问∠E=∠F吗？请说明理由．发布：2025/6/23 8:30:2组卷：124引用：3难度：0.3 -
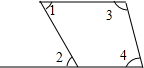2．如图，∠1=∠2，∠3=100°，则∠4=．发布：2025/6/23 9:0:1组卷：523引用：17难度：0.9 -
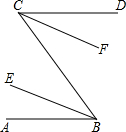3．在下列解题过程的空白处填上适当的内容（推理的理由或数学表达式）
如图，已知AB∥CD，BE、CF分别平分∠ABC和∠DCB，求证：BE∥CF．
证明：
∵AB∥CD，（已知）
∴∠=∠．（）
∵，（已知）
∴∠EBC=∠ABC，（角的平分线定义）12
同理，∠FCB=．
∴∠EBC=∠FCB．（等式性质）
∴BE∥CF．（）发布：2025/6/23 7:0:1组卷：340引用：15难度：0.7
