已知△ABC，点M在CB的延长线上．
（1）【问题情景】如图1，求证：∠BAC=∠ABM-∠ACB．
证明：过A点作AH∥BC，请按照上述思路继续完成证明过程；
（2）【尝试运用】如图2，延长AB至D，过点D作DN∥BC，再作∠ACB的平分线，交∠NDA的邻补角的平分线于点E，请探究∠A与∠CED的数关系并证明你的结论；
（3）【拓广探索】如图3，P是平面内一点，且不在直线MB、ND、AB上，∠MBP=m,∠NDP=n,∠BPD的度数为多少？请直接写出答案 n-m或m-n或m+n或360°-m-nn-m或m-n或m+n或360°-m-n（用含m、n的式子表示）．
【考点】平行线的判定与性质．
【答案】n-m或m-n或m+n或360°-m-n
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/4 8:0:9组卷：106引用：4难度：0.5
相似题
-
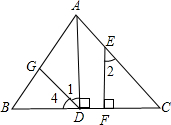1．已知，如图，AD⊥BC，EF⊥BC，∠4=∠C．求证：∠1=∠2．发布：2025/6/16 8:30:2组卷：800引用：11难度：0.5 -
2．下列说法：①内错角相等；②两条直线不平行必相交；③过一点有且只有一条直线与已知直线垂直；④平行于同一条直线的两条直线互相平行．其中错误的有（ ）
发布：2025/6/16 9:30:1组卷：87引用：3难度：0.7 -
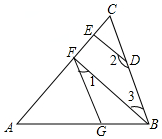3．完成下列说理过程：如图所示，DE⊥AC于点E，BF⊥AC于点F，∠1+∠2=180°，试说明∠AGF=∠ABC．
解：理由如下：
∵DE⊥AC，BF⊥AC（已知），
∴∠DEC=∠BFC=90°（）．
∴∥（）．
∴∠+∠3=180°（）．
又∵∠1+∠2=180°（已知），
∴∠1=∠3（）．
∴∥（内错角相等，两直线平行）．
∴∠AGF=∠ABC（）．发布：2025/6/16 10:0:1组卷：396引用：3难度：0.6
