在Rt△ABC中，AC=BC，∠ACB=90°，D为BC上一点．
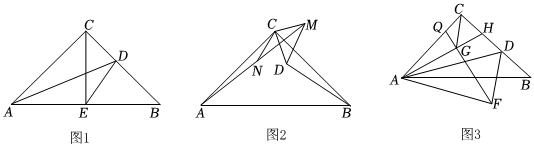
（1）如图1，过C作CE⊥AB于E，连接AD，DE．若AD平分∠BAC，CD=3，求DE的长；
（2）如图2，以CD为直角边，点C为直角顶点，向右作等腰直角△DCM，将△DCM绕点C顺时针旋转α°（0＜α＜45），连接AM，BD，取线段AM的中点N，连接CN．求证：BD=2CN；
（3）如图3，连接AD，将△ACD沿AD翻折至△ADF处，在BC上取点H，连接AH，过点F作FQ⊥AH交AC于点Q，FQ交AH于点G，连接CG，若FQ：AH=3：2，AB=4，当CG取得最小值时，求△ACG的面积．
3
【考点】三角形综合题．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/11 4:0:9组卷：383引用：4难度：0.2
相似题
-
1．特例感知：
如图1，在等边三角形ABC中，D是BC延长线上一点，且CD＜BC，以CD为边在上方作等边三角形CDE，连接BE，过点B作BF∥ED，过点D作DF∥BE，交于点F，连接AF．
（1）试判断AF和BE的数量关系，并说明理由．
猜想论证：
（2）将△CDE绕点C按顺时针方向旋转一定角度，其余操作不变，则AF和BE的数量关系是否仍然成立，请仅就图2的情形说明理由．
拓展延伸：
（3）将如图1所示的△CDE绕点C按逆时针方向旋转α（0°＜α＜90°），其余操作不变．若=BCCD，当△ABF是直角三角形时，请直接写出α的值．2
发布：2025/5/23 6:30:1组卷：320引用：5难度：0.2 -
2．综合与实践二轮复习中，刘老师以“最值问题”为专题引导同学们进行复习探究．
问题模型：等腰三角形ABC，∠BAC=120°，AB=AC=2．
探究1：
（1）如图1，点D为等腰三角形ABC底边BC上一个动点，连接AD，则AD的最小值为 ，判断依据为 ；
探究2：
（2）在探究1的结论下，继续探究，作∠BAD的平分线AE交BC于点E，点F，G分别为AE，AD上一个动点，求DF+FG的最小值；
探究3
（3）探究在探究1的结论下，继续探究，点M为线段CD上一个动点，连接AM，将AM顺时针旋转 60°，得到线段AN，连接ND，求线段DN的最小值.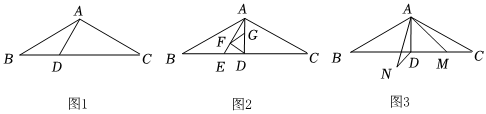
发布：2025/5/23 6:0:2组卷：331引用：4难度：0.2 -
3．已知等边三角形ABC，过A点作AC的垂线l,P为l上一动点（不与点A重合），连接CP，将线段CP绕点C逆时针旋转60°得到CQ，连接QB．
（1）如图1，直接写出线段AP与BQ的数量关系；
（2）如图2，当点P，B在AC同侧，连接PB并延长，与CQ交于点D，若AP=AC，求证：线段PD垂直平分CQ；
（3）如图3，某地河堤路l旁有一边长为4的等边三角形花圃ABC，且AC边垂直于路l,市政部门计划在河堤路另一侧修建一个三角形的观景平台APQ，要求点P，B分别位于AC边的异侧，连接CP，将线段CP绕点C逆时针旋转60°得到CQ，再连接AQ和PQ，若三角形观景平台APQ的面积等于，求此时AP的长度．34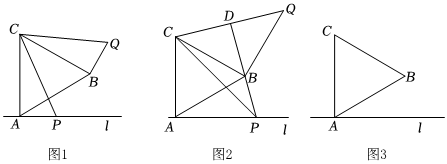
发布：2025/5/23 6:0:2组卷：100引用：1难度：0.3
