如图1:在⊙O中,AB为直径,C是⊙O上一点,AC=3,BC=4.过O分别作OH⊥BC于点H,OD⊥AC于点D,点E、F分别在线段BC、AC上运动(不含端点),且保持∠EOF=90°.
(1)OC=2.52.5;四边形CDOH是 矩形矩形(填矩形/菱形/正方形);S四边形CDOH=33;
(2)当F和D不重合时,求证:△OFD∽△OEH;
(3)①在图1中,⊙P是△CEO的外接圆,设⊙P面积为S,求S的最小值,并说明理由;
②如图2:若Q是线段AB上一动点,且QA:QB=1:n,∠EQF=90°,⊙M是四边形CEQF的外接圆,则当n为何值时,⊙M的面积最小?最小值为多少?请直接写出答案.

【考点】圆的综合题.
【答案】2.5;矩形;3
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/7/10 8:0:8组卷:208引用:1难度:0.5
相似题
-
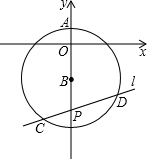 1.如图,圆心B在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1).过点P(0,-7)的直线l与⊙B相交于C、D两点,则弦CD长的所有可能的整数值有个;它们是.发布:2025/6/18 10:30:1组卷:365引用:2难度:0.7
1.如图,圆心B在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1).过点P(0,-7)的直线l与⊙B相交于C、D两点,则弦CD长的所有可能的整数值有个;它们是.发布:2025/6/18 10:30:1组卷:365引用:2难度:0.7 -
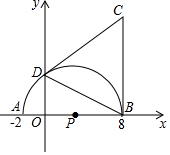 2.如图,平面直角坐标系中,A(-2,0),B(8,0),以AB为直径作半圆P交y轴于点D,过点B作BC⊥x轴,且BC=10,连接CD.
2.如图,平面直角坐标系中,A(-2,0),B(8,0),以AB为直径作半圆P交y轴于点D,过点B作BC⊥x轴,且BC=10,连接CD.
(1)图中⊙P的半径长为,点D的坐标为;
(2)求证:直线CD是⊙P的切线;
(3)求tan∠CDB的值.发布:2025/6/18 13:0:8组卷:103引用:1难度:0.5 -
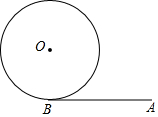 3.如图,已知⊙O的半径为3,A是⊙O外一点,AB切⊙O于点B,且AB=6.
3.如图,已知⊙O的半径为3,A是⊙O外一点,AB切⊙O于点B,且AB=6.
(1)求点A到⊙O上的点之间的最短距离;
(2)作AB的中垂线CD交AB于C,试判断CD与⊙O的位置关系,并证明;
(3)若⊙O上点M能与AB构成等腰三角形,请直接写出所有符合条件的BM的值.发布:2025/6/18 13:0:8组卷:256引用:1难度:0.1


