已知椭圆C：x2a2+y2b2=1（a＞b＞0）的焦点是（-3，0）、（3，0），且由椭圆上顶点、右焦点和原点组成的三角形面积为32．
（1）求椭圆C的方程；
（2）设P（0，4），M、N是椭圆C上关于y轴对称的任意两个不同的点，连接PN交椭圆C于另一点E，证明：直线ME与y轴相交于定点．
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
3
3
3
2
【考点】直线和圆的方程的应用．
【答案】（1）+y2=1；
（2）设N（x1，y1）、E（x2，y2）、M（-x1，y1），
直线PN的方程为y=kx+4，则
由
，消去y得：
（1+4k2）x2+32kx+60=0…
由根与系数的关系，得
x1+x2=，x1x2=…
∴直线lME的方程为y-y1=（x+x1）；…
∴当x=0时，y=+y1
=
=
=
=+4
=；…
∴直线ME与y轴相交于定点．
x
2
4
（2）设N（x1，y1）、E（x2，y2）、M（-x1，y1），
直线PN的方程为y=kx+4，则
由
x 2 4 + y 2 = 1 |
y = kx + 4 |
（1+4k2）x2+32kx+60=0…
由根与系数的关系，得
x1+x2=
-
32
k
1
+
4
k
2
60
1
+
4
k
2
∴直线lME的方程为y-y1=
y
2
-
y
1
x
2
+
x
1
∴当x=0时，y=
（
y
2
-
y
1
）
x
1
x
1
+
x
2
=
x
1
y
2
+
x
2
y
1
x
1
+
x
2
=
x
2
（
kx
1
+
4
）
+
x
1
（
kx
2
+
4
）
x
1
+
x
2
=
2
kx
1
x
2
+
4
（
x
1
+
x
2
）
x
1
+
x
2
=
120
-
32
=
1
4
∴直线ME与y轴相交于定点
（
0
，
1
4
）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/5 8:0:8组卷：167引用：4难度：0.1
相似题
-
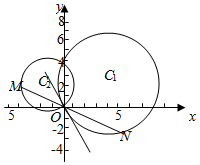1．已知圆C1：（x-4）2+（y-2）2=20与y轴交于O，A两点，圆C2过O，A两点，且直线C2O与圆C1相切；
（1）求圆C2的方程；
（2）若圆C2上一动点M，直线MO与圆C1的另一交点为N，在平面内是否存在定点P使得PM=PN始终成立，若存在求出定点坐标，若不存在，说明理由．发布：2024/10/16 15:0:1组卷：547引用：7难度：0.3 -
2．若直线ax+y=0始终平分圆x2+y2-2ax+2ay+2a2+a-1=0的周长，则a的值为（ ）
发布：2024/12/8 10:30:3组卷：358引用：2难度：0.8 -
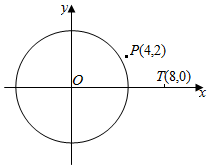3．已知直角坐标系xOy中，圆O：x2+y2=16．
①过点P（4，2）作圆O的切线m,求m的方程；
②直线l：y=kx+b与圆O交于点M，N两点，已知T（8，0），若x轴平分∠MTN，证明：不论k取何值，直线l与x轴的交点为定点，并求出此定点坐标．发布：2024/9/25 3:0:1组卷：148引用：2难度：0.6
