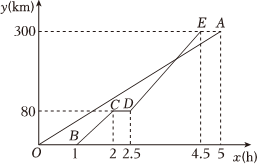
甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地，如图，是它们离甲地距离y（千米）与时间x（小时）之间的函数关系图象，请根据图象解答下列问题：
（1）线段CD表示轿车在途中停留了 0.50.5小时；
（2）求线段OA和线段DE的解析式；
（3）当货车与轿车和甲地等距离时，轿车在行驶过程中所用的时间是多少？
【考点】一次函数的应用．
【答案】0.5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/31 8:0:9组卷：52引用：1难度：0.6
相似题
-
1．某通讯公司推出了移动电话的两种计费方式，设一个月内使用移动电话主叫的时间为x分钟（x≥0），方式一，方式二的月使用费用分别为y1元，y2元，两种计费方式被叫均免费．其中方式一月使用费详情见下表，方式二的月使用费y2元与主叫时间x分钟的函数图象如图所示．
月使用费/元 主叫限定时间/分钟 主叫超时费/（元/分钟） 被叫 方式一 38 120 0.1 免费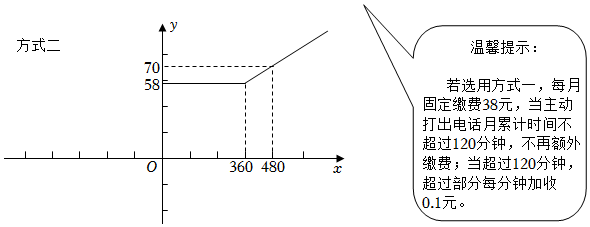 
（1）根据题意填表：
表格一：
表格二：主叫时间x分钟 x=100 x=320 x˃120 方式一计费/元
（2）结合图象信息，求y2与x的函数解析式，并写出自变量x的取值范围；月使用费/元 主叫限定时间/分钟 主叫超时费/（元/分钟） 被叫 方式二 免费
（3）选用哪种计费方式花费少（直接写出结果即可）．发布：2025/6/13 12:30:10组卷：103引用：1难度：0.5 -
2．某健身房暑假期间面对大学生推出健身优惠月活动，活动方案如下：
方案一：不购买会员卡健身，每次收费10元；
方案二：购买会员卡健身，需交会员费120元，每次另收费4元；
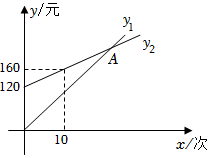
设大学生健身次数为x（次），按照方案一所需费用为y1（元），且y1=k1x（k1≠0）；按照方案二所需费用为y2（元），且y2=k2x+b（k2≠0）．其函数图象如图所示．
（1）填空：k1=，k2=，b=；
（2）两种方案的函数图象交于点A，请直接写出A点的坐标；
（3）若某同学暑假期间准备健身30次，选择哪种方案所需费用较少？少多少？发布：2025/6/13 15:0:2组卷：333引用：1难度：0.7 -
3．如图，一条笔直的公路上依次有A、B、C三个村庄，甲从A村匀速骑自行车到B村，乙从C村经B村匀速骑摩托车到A处，两人同时出发，到达各自终点后立即停止运动．设甲骑车的时间为x h,甲、乙两人离A村的距离为y km,y与x之间的函数关系如图所示，则下列说法错误的是（ ）发布：2025/6/13 12:30:10组卷：165引用：1难度：0.6
