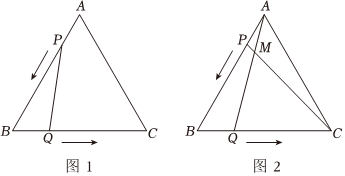
如图①，已知△ABC是边长为3cm的等边三角形，动点P从点A出发，沿AB边匀速运动；同时，动点Q从点B出发，沿BC边匀速运动．它们的速度都是1cm/s,当点P到达点B时，P、Q两点都停止运动，设点P的运动时间为t（s）．
（1）BQ的长为 ttcm,BP的长为 （3-t）（3-t）cm（用含t的式子表示）；
（2）求当t为何值时，△PBQ是直角三角形？
（3）如图②，连接AQ、CP相交于点M，则点P、Q在运动的过程中，∠CMQ的大小会变化吗？若变化，请说明理由；若不变，请求出它的度数．
【考点】三角形综合题．
【答案】t；（3-t）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/14 2:0:2组卷：90引用：1难度：0.1
相似题
-
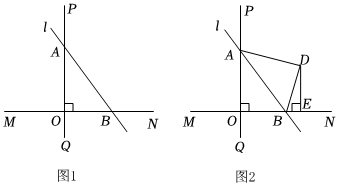1．如图1，直线MN⊥PQ，垂足为O，直线l分别与射线OP、ON相交于点A、B，且OA=4，OB=3，连接AB．
（1）求线段AB的长；
（2）若点C为直线l上的一个动点，求点O到点C的距离的最小值；
（3）如图2，将△AOB沿直线l折叠，点O落在点D处，DE⊥MN，垂足为点E，求DE的长；
（4）若点F为直线MN或PQ上的一个动点，使得以A、B、F为顶点的三角形是等腰三角形，则满足条件的所有点F的个数为 个．发布：2025/6/9 0:30:2组卷：199引用：2难度：0.1 -
2．如图1，△ACB和△ECD都是等腰直角三角形，CA=CB，CE=CD．
（1）[教材呈现]△ACB的顶点A在△ECD的斜边DE上，线段AE、AD、AC之间的数量关系为 ．
（2）[变换探究]如图2，△ACB的顶点A在△ECD的斜边DE的延长线上，且CA=CB=3，CE=CD=22，求线段AE的长．2
（3）[拓展应用]如图3，△ACB的顶点A在△ECD的斜边DE上运动（不与D、E重合），若CE=CD=2，问△ABD的面积是否有最大值？如果有，请求出这个最大值，如果没有，请说明理由．2
发布：2025/6/9 1:0:1组卷：65引用：1难度：0.3 -
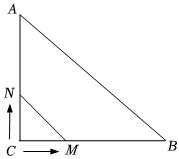3．如图，在Rt△ACB中，∠C=90°，AC+AB=8，点M从点C开始，沿C→B→C的路径运动，点N从点C开始，沿着C→A→B的路径运动，且速度都是每秒1个单位，点M与点N同时从点C开始运动，且同时到达各自终点并停止运动．
（1）填空：AC=；
（2）设运动时间t秒（t＞0），若连接AM，当t为何值时，AM=BM；
（3）设运动时间t秒（t＞0），若线段MN的垂直平分线过△ACB的顶点时，请直接写出符合要求的t的范围 ．发布：2025/6/9 1:0:1组卷：168引用：3难度：0.3
