题目：求证：平行四边形的两组对边分别相等．
已知：如图，四边形ABCD是平行四边形．
求证：AB=CD，BC=DA．
证明：连结BD，
∵四边形ABCD是平行四边形，
∴……，
∴∠CDB=∠ABD．
∵AD∥BC，
∴∠CBD=∠ADB．
∵……，
∴△ABD≌△CDB．
∴AB=CD，AD=CB．
其中，在“……”处应补充的步骤依次是（ ）
【考点】平行四边形的判定与性质；全等三角形的判定．
【答案】D
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：83引用：1难度：0.5
相似题
-
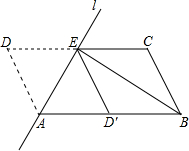1．如图，将▱ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处，折痕l交CD边于点E，连接BE．
（1）求证：四边形BCED′是平行四边形；
（2）若BE平分∠ABC，求证：AB2=AE2+BE2．发布：2025/6/23 11:0:1组卷：8574引用：80难度：0.5 -
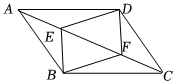2．已知，如图，在▱ABCD中，E、F是对角线AC上的两点，且AE=CF．
求证：四边形BEDF是平行四边形．发布：2025/6/22 20:30:1组卷：226引用：9难度：0.5 -
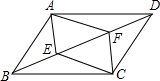3．如图，在▱ABCD中，E、F是对角线BD上两点，且BE=DF，连接AE、CE、AF、CF，四边形AECF是平行四边形吗？为什么？发布：2025/6/23 9:30:1组卷：52引用：2难度：0.5
