综合与实践
问题提出
如图1，在四边形ABCD中，E，F，G，H分别是AB，BD，CD，AC的中点，求证：四边形EFGH是平行四边形．
探究展示
某学习小组的解题思路如图3：
反思交流
（1）上述解题思路中的“依据1”、“依据2”分别是什么？
依据1：三角形的中位线平行于第三边，且等于第三边的一半三角形的中位线平行于第三边，且等于第三边的一半．
依据2：一组对边平行且相等的四边形是平行四边形一组对边平行且相等的四边形是平行四边形．
（2）若四边形ABCD满足“AD=BC”的条件，试判断四边形EFGH的形状，并说明理由．
（3）要使四边形EFGH为矩形，则四边形ABCD需满足的条件是：AD⊥CBAD⊥CB．
拓展思考
（4）如图2，△BAC和△DAE都是等腰直角三角形，∠BAC=∠DAE=90°，点F，G分别是BC，DE的中点，连接BD，CE．请用等式表示BD与FG的数量关系，并证明．
【考点】四边形综合题．
【答案】三角形的中位线平行于第三边，且等于第三边的一半；一组对边平行且相等的四边形是平行四边形；AD⊥CB
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/29 8:0:10组卷：98引用：1难度：0.5
相似题
-
1．[证明体验]
（1）如图1，在△ABC中，点D在边BC上，点F在边AC上，AB=AD，FB=FC，AD与BF相交于点E．求证：∠ABF=∠CAD．
[思考探究]
（2）如图2，在（1）的条件下，过点D作AB的平行线交AC于点G，若DE=2AE，AB=6，求DG的长．
[拓展延伸]
（3）如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，∠ABC=∠ACB=67.5°，OD=2OB，OA=，求CD的长．2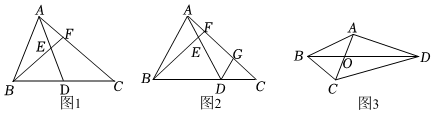
发布：2025/5/23 23:30:1组卷：687引用：3难度：0.3 -
2．问题提出
（1）如图①，△ABC是等腰三角形，点D，E分别在腰AC，AB上，且BE=CD，连接BD，CE．则BD与CE长度的大小关系是BD CE（填“＞”“＜”或“=”）；
问题探究
（2）如图②，AD是△ABC的中线，BE交AC于E，交AD于F，若AE=EF，AC=8，求线段BF的长；
问题解决
（3）党的二十大报告提出全面推进乡村振兴，坚持农业农村优先发展．某地区规划出如图③所示的四边形ABCD地块，计划开发出一个生态宜居，绿色人文的农业观光区，其中AD⊥CD，BC⊥CD，∠BAD=120°，点E是BC上的一个休息站，CE=AB，AE是一条林荫小道．为使游客方便参观，现要修建木制栈道BP与玻璃栈道AC，点P是AE的中点．已知木制栈道每米的造价是a元，玻璃栈道每米的造价是3a元，请问修建玻璃栈道的总费用是修建木制栈道总费用的几倍？并说明理由．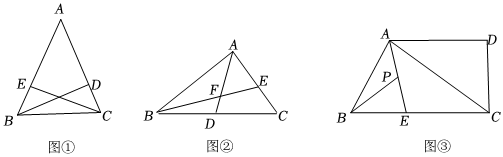
发布：2025/5/24 0:30:1组卷：169引用：2难度：0.2 -
3．【问题情境】
（1）同学们我们曾经研究过这样的问题：已知正方形ABCD，点E在CD的延长线上，以CE为一边构造正方形CEFG，连接BE和DG，如图1所示，则BE和DG的数量关系为，位置关系为．
【继续探究】
（2）若正方形ABCD的边长为4，点E是AD边上的一个动点，以CE为一边在CE的右侧作正方形CEFG，连接DG、BE，如图2所示，
①请判断线段DG与BE有怎样的数量关系和位置关系，并说明理由；
②连接BG，若AE=1，求线段BG长．爱动脑筋的小丽同学是这样做的：过点G作GH⊥BC，如图3，你能按照她的思路做下去吗？请写出你的求解过程．
【拓展提升】
（3）在（2）的条件下，点E在AD边上运动时，利用图2，则BG+BE的最小值为．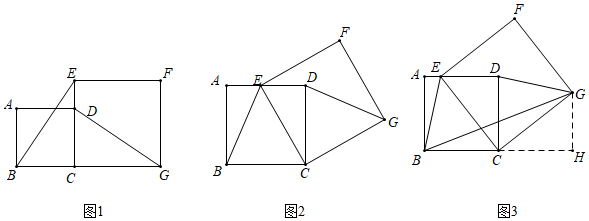
发布：2025/5/24 0:30:1组卷：1979引用：10难度：0.1
