综合与实践：
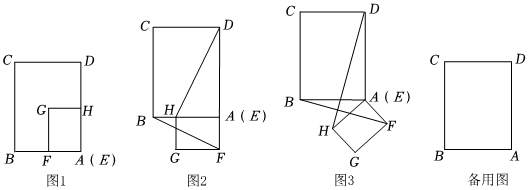
【问题情境】在数学活动课上，王老师让同学们用两张矩形纸片进行探究活动．阳光小组准备了两张矩形纸片ABCD和EFGH、其中AB=6，AD=8，将它们按如图所示的方式放置，当点A与点E重合，点F，H分别落在AB，AD边上时，点F，H恰好为边AB．AD的中点，然后将矩形纸片EFGH绕点A按逆时针方向旋转，旋转角为α，连接BF与DH．
【观察发现】如图2．当α=90° 时，小组成员发现△BAF∽△DAH，易得BFDH=34，DH⊥BF．
【探索猜想】（1）如图3，当90°＜α＜180°时，【观察发现】中发现的结论BFDH=34，DH⊥BF是否仍然成立？请说明理由．
【拓展延伸】（2）在矩形EFGH旋转过程中，当C，A，F三点共线时，请求出线段DH的长．
BF
DH
=
3
4
BF
DH
=
3
4
【考点】相似形综合题．
【答案】（1）当90°＜α＜180°时，（1）中发现的结论仍然成立，理由见解答过程；
（2）或．
（2）
4
5
185
4
5
65
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 8:0:10组卷：119引用：1难度：0.5
相似题
-
1．在△ABC中，AB=AC，∠BAC=90°，点D，E分别是AC，BC的中点，点P是射线DE上一点，连接AP，将线段PA绕点P顺时针旋转90°得到线段PM，连接AM，CM．
（1）如图①，当点P与点D重合时，线段CM与PE的数量关系是 ，∠ACM=°；
（2）如图②当点P在射线DE上运动时（不与点D，E重合），求的值；PECM
（3）连接PC，当△PCM是等边三角形时，请直接写出的值．ACCM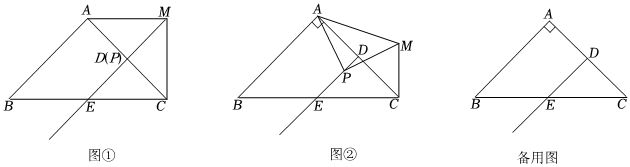
发布：2025/5/23 0:30:1组卷：370引用：2难度：0.1 -
2．已知△ABC是等边三角形，D是直线AB上的一点．
（1）问题背景：如图1，点D，E分别在边AB，AC上，且BD=AE，CD与BE交于点F，求证：∠EFC=60°；
（2）点G，H分别在边BC，AC上，GH与CD交于点O，且∠HOC=60°．
①尝试运用：如图2，点D在边AB上，且，求OHOG=43的值；ABBD
②类比拓展：如图3，点D在AB的延长线上，且，直接写出OHOG=256的值．ABBD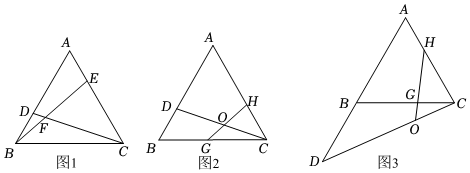
发布：2025/5/23 1:0:1组卷：822引用：3难度：0.2 -
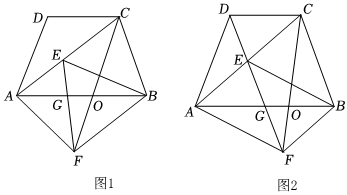3．如图1，AB=AC=2CD，DC∥AB，将△ACD绕点C逆时针旋转得到△FCE，使点D落在AC的点E处，AB与CF相交于点O，AB与EF相交于点G，连接BF．
（1）求证：△ABE≌△CAD；
（2）求证：AC∥FB；
（3）若点D，E，F在同一条直线上，如图2，求的值．（温馨提示：请用简洁的方式表示角）ABBC发布：2025/5/23 1:0:1组卷：363引用：2难度：0.4
