某工厂计划从现在开始，在每个生产周期内生产并销售完某型号设备，该设备的生产成本为10万元/件．设第x个生产周期设备的售价为z万元/件，售价z与x之间的函数解析式是z=15，0＜x≤12 mx+n,12＜x≤20
，其中x是正整数．当x=16时，z=14；当x=20时，z=13．
（1）求m,n的值；
（2）设第x个生产周期生产并销售完设备的数量为y件，且y与x满足关系式y=5x+20．
①当12＜x≤20时，工厂第几个生产周期获得的利润最大？最大的利润是多少万元？
②当0＜x≤20时，若有且只有3个生产周期的利润不小于a万元，求实数a的取值范围．
15 ， 0 ＜ x ≤ 12 |
mx + n , 12 ＜ x ≤ 20 |
【考点】二次函数的应用．
【答案】（1）m=-，n=18；
（2）①工厂第14个生产周期获得的利润最大，最大的利润是405万元；
②a的取值范围400＜a≤403.75．
1
4
（2）①工厂第14个生产周期获得的利润最大，最大的利润是405万元；
②a的取值范围400＜a≤403.75．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/1 8:0:9组卷：1638引用：7难度：0.4
相似题
-
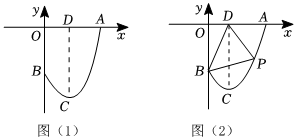1．如图（1），一块钢板余料截面的两边为线段OA，OB，另一边曲线ACB为抛物线的一部分，其中C点为抛物线的顶点，CD⊥OA于D，以OA边所在直线为x轴，OB边所在直线为y轴，建立平面直角坐标系xOy,规定一个单位代表1米．已知OD=1米，DA=2米，CD=4米．
（1）求曲线ACB所在抛物线的函数表达式；
（2）若在该钢板余料中截取一个一边长为3米的矩形，设该矩形的另一边长为h米，求h的取值范围；
（3）如图（2），若在该钢板余料中截取一个△PBD，其中点P在抛物线ACB上，记△PBD的面积为S，求S的最大值．发布：2025/5/23 16:0:1组卷：103引用：1难度：0.5 -
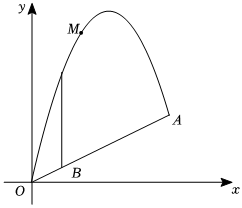2．如图，一小球M从斜坡OA上的O点处抛出，建立如图所示的平面直角坐标系，球的抛出路线是抛物线L1：y=-+bx的一部分，斜坡可以看作直线L2：y=12x2x的一部分．若小球经过点（6，6），解答下列问题：12
（1）求抛物线L1的表达式，并直接写出抛物线L1的对称轴；
（2）小球在斜坡上的落点为A，求A点的坐标；
（3）在斜坡OA上的B点有一棵树，B点的横坐标为2，树高为4，小球M能否飞过这棵树？通过计算说明理由；
（4）直接写出小球M在飞行的过程中离斜坡OA的最大高度．发布：2025/5/23 16:30:1组卷：329引用：3难度：0.5 -
3．【综合实践】
某公园在人工湖里安装一个喷泉，在湖心处竖直安装一根水管，在水管的顶端安一个喷水头，喷出的水柱形状可以看作是抛物线的一部分．若记水柱上某一位置与水管的水平距离为x米，与湖面的垂直高度为y米．下面的表中记录了x与y的五组数据：
（1）在下面网格（图1）中建立适当的平面直角坐标系，并根据表中所给数据画出表示y与x函数关系的图象；x（米） 0 1 2 3 4 y（米） 0.5 1.25 1.5 1.25 0.5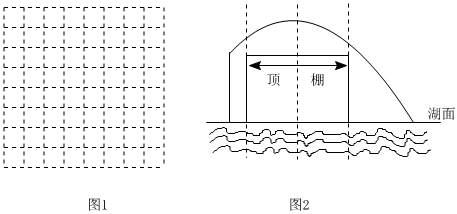 
（2）若水柱最高点距离湖面的高度为m米，则m=，并求y与x函数表达式；
（3）现公园想通过喷泉设立新的游玩项目，准备通过只调节水管露出湖面的高度，使得游船能从抛物线形水柱下方通过，如图2所示，为避免游船被喷泉淋到，要求游船从抛物线形水柱下方中间通过时，顶棚上任意一点到水柱的竖直距离均不小于0.5米，已知游船顶棚宽度为3米，顶棚到湖面的高度为2米，那么公园应将水管露出湖面的高度（喷水头忽略不计）至少调节到多少米才能符合要求？请通过计算说明理由（结果保留一位小数）．发布：2025/5/23 16:30:1组卷：1253引用：4难度：0.5
