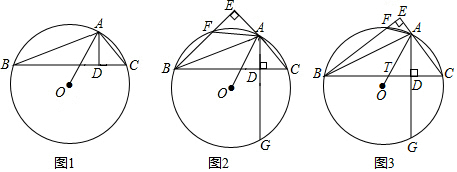
△ABC内接⊙O，AD⊥BC与D，连接OA．
（1）如图1，求证：∠BAO=∠CAD；
（2）如图2，作BE⊥AC交CA延长线于E交⊙O于F，延长AD交⊙O于G，连接AF，求证：AD+AF=DG；
（3）在第（2）问的条件下，如图3，OA交BC于点T，CA=CT，AD=2AF，AB=45，求DT长．
5
【考点】圆的综合题．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/26 0:0:1组卷：416引用：3难度：0.3
相似题
-
1．如图，点P是等边三角形ABC的AC边上的动点（0°＜∠ABP＜30°），作△BCP的外接圆⊙O交AB于D．点E是⊙O上一点，且=ˆPD，连结DE，BE，CE，且DE交BP于F．ˆPE
（1）求证：∠ADE=∠BEC；
（2）当点P运动变化时，∠BFD的度数是否变化？若变化，请说明理由；若不变，求∠BFD的度数；
（3）探究线段BF，CE，EF间的数量关系，并证明．发布：2025/5/23 2:30:1组卷：233引用：1难度：0.3 -
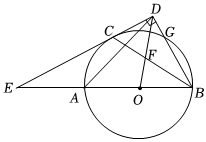2．如图，AB是⊙O的直径，C、G是⊙O上两点，且，过点C的直线CD⊥BG于点D，交BA的延长线于点E，连接BC，交OD于点F．ˆAC=ˆCG
（1）求证：CD是⊙O的切线．
（2）若，求∠E的度数．OFFD=23
（3）连接AD，在（2）的条件下，若CD=，求AD的长．3发布：2025/5/23 3:0:1组卷：286引用：1难度：0.9 -
3．如图，在△ABC中，∠ACB=90°，AC=4，BC=3．点O是边AB上的一个动点，以O为圆心作半圆，与边AC相切于点D，交线段OB于点E，过点E作EG⊥DE，交射线AC于点G，交射线BC于点F．
（1）求证：∠ADE=∠AEG；
（2）设OA=x,CF=y,求y关于x的函数解析式，并写出x的取值范围；
（3）BM为半圆O的切线，M为切点，当BM∥DE时，求OA的长．发布：2025/5/23 3:30:1组卷：431引用：2难度：0.3
