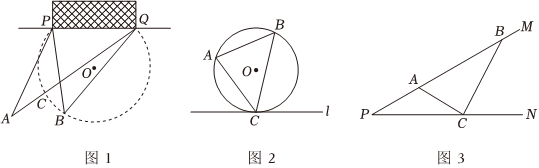
（1）如图1，在足球比赛场上，甲带球奔向对方球门PQ，当他带球冲到A点时，同伴乙已冲到B点，甲是自己射门好，还是将球传给乙，让乙射门好？
对上面这个问题，小明结合图1判断甲的视角∠PAQ小于乙的视角∠PBQ，根据“仅从射门角度考虑，球员对球门的视角越大，足球越容易被踢进”的经验，认为甲应该将球传给乙．请结合图1给出小明得到∠PAQ＜∠PBQ的理由；
（2）德国数学家米勒曾提出最大视角问题，并得到这样的结论：如图2，点A，B是平面内两个定点，C是直线l上的一个动点，当且仅当△ABC的外接圆与l相切于点C时，∠ACB最大．
如图3，∠MPN=30°，点A，B是边PM上两点，AB=6，点C是边PN上一动点．
①若∠ACB最大为90°，请求出当∠ACB=90°时，PC的长；
②若∠ACB最大不超过60°，直接写出PA的取值范围．
【考点】圆的综合题．
【答案】（1）说明理由见解析；（2）①3；②PA≥4．
3
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/13 0:0:1组卷：424引用：2难度：0.4
相似题
-
1．如图，AB是圆O的直径，弦CD与AB交于点H，∠BDC=∠CBE．
（1）求证：BE是圆O的切线；
（2）若CD⊥AB，AC=2，BH=3，求劣弧BC的长；
（3）如图，若CD∥BE，作DF∥BC，满足BC=2DF，连接FH、BF，求证：FH=BF．发布：2025/1/28 8:0:2组卷：100引用：1难度：0.1 -
2．如图，AB是圆O的直径，AB=6，D是半圆ADB上的一点，C是弧BD的中点．
（1）若∠ABD=30°，求BC的长和由弦BC、BD、和弧CD围成的图形面积；
（2）若弧AD的度数是120度，在半径OB上是否存在点P，使得PC+PD的值最小，如果存在，请在备用图中画出P的位置，并求PC+PD的最小值，如果不存在，请说明理由．
发布：2025/1/28 8:0:2组卷：44引用：0难度：0.3 -
3．如图，AB是圆O的直径，弦CD⊥AB于G，射线DO与直线CE相交于点E，直线DB与CE交于点H，且∠BDC=∠BCH．
（1）求证：直线CE是圆O的切线．
（2）如图1，若OG=BG，BH=1，直接写出圆O的半径；
（3）如图2，在（2）的条件下，将射线DO绕D点逆时针旋转，得射线DM，DM与AB交于点M，与圆O及切线CF分别相交于点N，F，当GM=GD时，求切线CF的长．
发布：2025/1/28 8:0:2组卷：782引用：2难度：0.1
