【操作发现】如图,现有1×1,1×a,1×b,a×b的矩形卡片各一张,请你在下面的方框内将它们拼成一个大的矩形(要求:画出分割线,并标注必要的线段长).观察操作前后的面积可以得到一个等式,这个等式是 a+b+ab+1=(a+1)(b+1)a+b+ab+1=(a+1)(b+1).

【应用探究】对于一个正整数n,若能找到正整数a,b,使得n=a+b+ab,则称n为一个“奇妙数”.例如3=1+1+1×1,则3就是一个“奇妙数”.根据“奇妙数”的规定,解决下列问题:
(1)7是不是一个“奇妙数”?为什么?
(2)从1到15这15个正整数中“奇妙数”有哪些?
【活动拓展】在一次数学活动课上,黑板上写有1、12、13、14、…、160共60个数字.小王老师要求同学们进行以下操作:每次操作先从黑板上的数中任选取2个数a、b,然后删去这两个数a和b,同时在黑板上写出与a+b+ab的值相等的数.试求经过59次操作后黑板上剩下的数.
1
2
1
3
1
4
1
60
【答案】a+b+ab+1=(a+1)(b+1)
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/7/11 8:0:9组卷:77引用:1难度:0.5
相似题
-
 1.在我校举行九年的级季篮球赛上,九年级(1)班的啦啦队队员,为了在明天的比赛中给本班同学加油助威,提前每人制作了一面同一规格的直角三角形彩旗.队员小明放学回家后,发现自己的彩旗破损了一角,他想重新制作一面彩旗.请你帮助小明,用直尺与圆规在作出一个与破损前完全一样的三角形(保留作图痕迹,不写作法).发布:2025/6/24 18:0:1组卷:29引用:2难度:0.5
1.在我校举行九年的级季篮球赛上,九年级(1)班的啦啦队队员,为了在明天的比赛中给本班同学加油助威,提前每人制作了一面同一规格的直角三角形彩旗.队员小明放学回家后,发现自己的彩旗破损了一角,他想重新制作一面彩旗.请你帮助小明,用直尺与圆规在作出一个与破损前完全一样的三角形(保留作图痕迹,不写作法).发布:2025/6/24 18:0:1组卷:29引用:2难度:0.5 -
2.图①、图②均是6×6的正方形网格,每个小正方形的顶点称为格点,线段AB的点均在格点上,在图①、图②给定的网格中按要求画图.要求:借助网格,只用无刻度的尺,不要求写出画法.
(1)在图①中找到一个格点C,使∠ABC是锐角,且tan∠ABC=,并画出△ABC;14
(2)在图②中找到一个格点D,使∠ADB是锐角,且tan∠ADB=1,并画出△ABD. 发布:2025/6/25 4:0:1组卷:17引用:1难度:0.5
发布:2025/6/25 4:0:1组卷:17引用:1难度:0.5 -
3.图①、图②、图③均是8×8的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、B、C均在格点上.在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,不要求写出画法,保留作图痕迹.
(1)在图①中画出△ABC的中线BD.
(2)在图②△ABC的边AB上找到一点E,将AB分成2:3两部分.
(3)在图③△ABC的边BC上找到一点F,使S△ABF:S△ACF=2:3.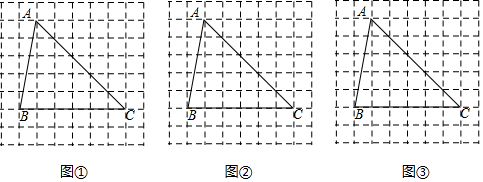 发布:2025/6/25 5:30:3组卷:644引用:6难度:0.1
发布:2025/6/25 5:30:3组卷:644引用:6难度:0.1


