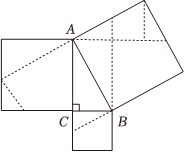
我国后汉时期的数学家赵爽利用弦图证明了勾股定理，这种利用面积出入相补证明勾股定理的方法巧妙又简便，对于勾股定理我国历史上有多位数学家创造了不同的面积政法，如魏晋时期的刘徽、清代的梅文鼎、华蘅芳等．下图为华蘅芳证明勾股定理时构造的图形，若图中CB=1，CA=2，∠ABC=90°，以点C为原点，

CB

为x轴正方向．

CA

为y轴正方向，建立平面直角坐标系，以AB的中点D为圆心作圆D，使得图中三个正方形的所有顶点恰有2个顶点在圆D外部，则圆D的一个标准方程为

（

x

-

1

2

）

2

+

（

y

-

1

）

2

=

25

4

（答案不㫿一）

（

x

-

1

2

）

2

+

（

y

-

1

）

2

=

25

4

（答案不㫿一）

．（写出一个即可）