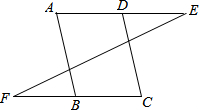
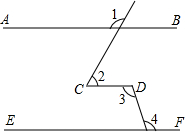
点E在射线AD上,点F、G为射线BC上两个动点,满足∠B=∠AEF,∠BAG=∠BGA,AG平分∠BAD.
(1)如图1,当点G在F右侧时,求证:AB∥EF;
(2)如图2,当点G在F左侧时,求证:∠AGE=∠BAG+∠FEG;
(3)如图3,在(2)的条件下,P为BA延长线上一点,AM平分∠BAG,交BC于点M,AN平分∠PAM,交EF于点N,连接NG,若∠ANG与∠GAN互余,∠B-∠ANG=∠EAN,求∠B的度数.
【答案】(1)证明见解答过程.
(2)证明见解答过程.
(3)答:∠B=60°.
(2)证明见解答过程.
(3)答:∠B=60°.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/19 8:0:9组卷:351引用:1难度:0.3