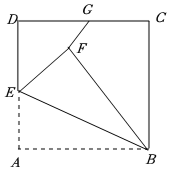
 如图,正方形ABCD的边长为10,点G是边CD的中点,点E是边AD上一动点,连接BE,将△ABE沿BE翻折得到△FBE,连接GF,则GF的最小值是( )
如图,正方形ABCD的边长为10,点G是边CD的中点,点E是边AD上一动点,连接BE,将△ABE沿BE翻折得到△FBE,连接GF,则GF的最小值是( )
【考点】翻折变换(折叠问题);正方形的性质.
【答案】A
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/5/20 8:0:9组卷:367引用:4难度:0.5
相似题
-
 1.将矩形ABCD沿折线EF折叠后点B恰好落在CD边上的点H处,且∠CHE=40°,则∠EFB=.发布:2025/6/24 18:30:1组卷:322引用:12难度:0.9
1.将矩形ABCD沿折线EF折叠后点B恰好落在CD边上的点H处,且∠CHE=40°,则∠EFB=.发布:2025/6/24 18:30:1组卷:322引用:12难度:0.9 -
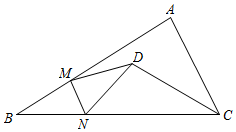 2.如图,在△ABC中,∠B=30°,M、N为边AB、BC上的两个动点,将△BMN沿MN翻折,翻折后点B的对应点D落在直线BC上方,连接CD,∠DCB=2∠AMD,且∠AMD>20°,则当△CDN是等腰三角形时,∠AMD=度.发布:2025/6/25 6:0:1组卷:381引用:2难度:0.6
2.如图,在△ABC中,∠B=30°,M、N为边AB、BC上的两个动点,将△BMN沿MN翻折,翻折后点B的对应点D落在直线BC上方,连接CD,∠DCB=2∠AMD,且∠AMD>20°,则当△CDN是等腰三角形时,∠AMD=度.发布:2025/6/25 6:0:1组卷:381引用:2难度:0.6 -
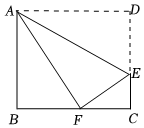 3.如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,若CF=4,tan∠EFC=,则折痕AE=( )34发布:2025/6/25 6:0:1组卷:94引用:2难度:0.7
3.如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,若CF=4,tan∠EFC=,则折痕AE=( )34发布:2025/6/25 6:0:1组卷:94引用:2难度:0.7


