综合与实践
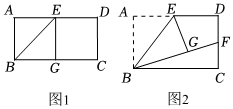
问题情境：在数学活动课上，数学老师让同学们用一张矩形纸片进行探究活动．小亮准备了矩形纸片ABCD，其中E是AD的中点，将△ABE沿BE折叠，点A的对应点为G．
观察发现：（1）如图1，当点G恰好在BC边上时，小亮发现AB与AD存在一定的数量关系，其数量关系是 AD=2ABAD=2AB．
探索猜想：（2）如图2，当点G在矩形ABCD内部时，延长BG交DC边于点F．试猜想线段BF，AB与DF之间的数量关系，并说明理由．
拓展延伸：（3）当点G在矩形ABCD内部时，若AD=3AB，直接写出线段DF与FC的数量关系．
AD
=
3
AB
【考点】四边形综合题．
【答案】AD=2AB
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/1 8:0:9组卷：89引用：6难度：0.3
相似题
-
1．在四边形ABCD中，∠A=∠B=90°，E为AB边上的点．
（1）连接CE，DE，CE⊥DE；
①如图1，若AE=BC，求证：AD=BE；
②如图2，若AE=BE，求证：CE平分∠BCD；
（2）如图3，F是∠BCD的平分线CE上的点，连接BF，DF，若BC=4，CD=6，，求CF的长．BF=DF=362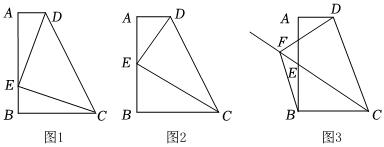
发布：2025/6/7 22:30:2组卷：95引用：2难度：0.1 -
2．阅读与应用：同学们：你们已经知道（a-b）2≥0，即a2-2ab+b2≥0．
∴a2+b2≥2ab（当且仅当a=b时取等号）．
阅读1：若a,b为实数，且a＞0，b＞0，∵（-a）2≥0，∴a-2b+b≥0．ab
∴a+b≥2（当且仅当a=b时取等号）．ab
阅读2：若函数y=x+（m＞0，x＞0，m为常数），由阅读1结论可知：mx
x+≥2mx即x+x•mx≥2mx，m
∴当x=，即x2=m,∴x=mx（m＞0）时，函数y=x+m的最小值为2mx．m
阅读理解上述内容，解答下列问题：
问题1：若函数y=a-1+（a＞1），则a=时，函数y=a-1+16a-1（a＞1）的最小值为 ；16a-1
问题2：已知一个矩形的面积为9cm,求此矩形周长的最小值；
问题3：求代数式（m＞-1）的最小值．m2+2m+10m+1发布：2025/6/7 23:30:2组卷：59引用：1难度：0.2 -
3．如图，四边形ABCD是正方形，点O为对角线AC的中点．
（1）问题解决：如图①，连接BO，分别取CB，BO的中点P，Q，连接PQ，则PQ与BO的数量关系是 ，位置关系是 ；
（2）问题探究：如图②，△AO'E是将图①中的△AOB绕点A按顺时针方向旋转45°得到的三角形，连接CE，点P，Q分别为CE，BO'的中点，连接PQ，PB．判断△PQB的形状，并证明你的结论；
（3）拓展延伸：如图③，△AO'E是将图①中的△AOB绕点A按逆时针方向旋转45°得到的三角形，连接BO'，点P，Q分别为CE，BO'的中点，连接PQ，PB．若正方形ABCD的边长为1，求△PQB的面积．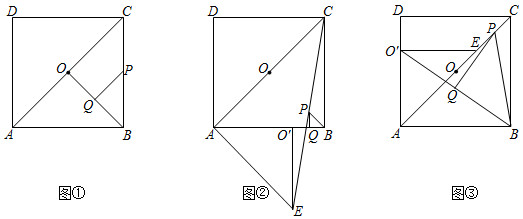
发布：2025/6/8 0:0:1组卷：2547引用：16难度：0.2
