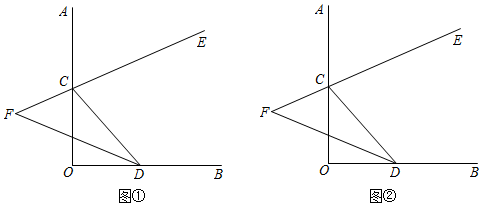
如图，∠AOB=90°，点C，D分别在射线OA，OB上，CE是∠ACD的平分线，CE的反向延长线与△CDO的平分线交于点F．
（1）若∠OCD=50°（图①），试求∠F；
（2）当C，D在射线OA，OB上任意移动时（不与点O重合）（如图②），∠F的大小是否变化？若变化，请说明理由；若不变化，请证明．
【考点】三角形内角和定理．
【答案】（1）45°．
（2）不变化，∠F=45°．分析见解析．
（2）不变化，∠F=45°．分析见解析．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/15 1:0:9组卷：355引用：1难度：0.8
相似题
-
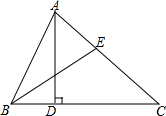1．如图，△ABC中，AD⊥BC于点D，BE平分∠ABC，若∠EBC=32°，∠AEB=70°．
（1）求∠BAD和∠CAD的度数；
（2）若点F为线段BC上的任意一点，当△EFC为直角三角形时，求∠BEF的度数．发布：2025/6/16 20:30:1组卷：575引用：6难度：0.3 -
2．如图：∠A+∠B+∠C+∠D+∠E+∠F等于 度．发布：2025/6/16 22:30:4组卷：480引用：27难度：0.9 -
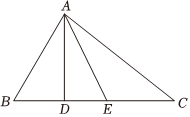3．已知：如图，在△ABC中，∠DAE=10°，AD⊥BC于点D，AE平分∠BAC，∠B=60°，求∠C的度数．发布：2025/6/16 21:0:1组卷：1494引用：7难度：0.8
