在矩形ABCD中．点E在BC的延长线上，且CE=CD，点F为DE边上一点，连接AF．作FG⊥AF交直线DC于点G．
（1）如图1，连接AG，若AB=BC，DF=EF时，判断△AFG的形状为等腰直角三角形等腰直角三角形．
（2）如图2，若AB=BC，DF≠EF时．试探究线段AD，DF，DG三者之间的数量关系，并证明你的结论．
（3）如图3，若AB≠BC，点F在ED的延长线上时，请先补全图形，再判断（2）的结论是否成立，若成立，请说明理由；若不成立．请直接写出新结论，不必证明．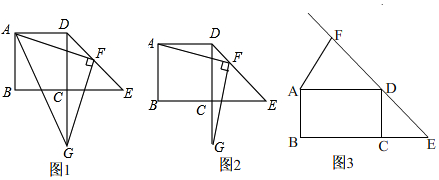
【考点】四边形综合题．
【答案】等腰直角三角形
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/7 8:0:9组卷：324引用：2难度：0.2
相似题
-
1．如图所示，△ABC为Rt△，∠ACB=90°，点D为AB的中点，点E为边AC上的点，连接DE，过点E作EF⊥ED交BC于F，以DE，EF为邻边作矩形DEFG，已知AC=8．
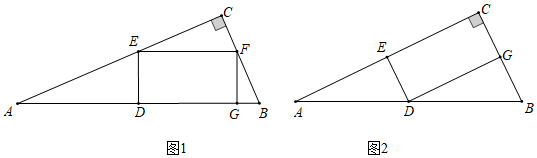
（1）如图1所示，当BC=6，点G在边AB上时，求DE的长．
（2）如图2所示，若，点G在边BC上时，求BC的长．DEEF=12
（3）①若，且点G恰好落在Rt△ABC的边上，求BC的长．DEEF=14
②若（n为正整数），且点G恰好落在Rt△ABC的边上，请直接写出BC的长．DEEF=12n发布：2025/5/24 2:0:8组卷：241引用：2难度：0.1 -
2．问题情境：
数学活动课上，同学们开展了以“矩形纸片折叠”为主题的探究活动（每个小组的矩形纸片规格相同），已知矩形纸片宽AB=8，长．AD=82
动手实践：
（1）如图1，腾飞小组将矩形纸片ABCD折叠，点A落在BC边上的点A'处，折痕为BE，连接A'E，然后将纸片展平，得到四边形AEA'B，则折痕BE的长为 ．
（2）如图2，永攀小组将矩形纸片ABCD沿经过A、C两点的直线折叠，展开后得折痕AC，再将其沿经过点B的直线折叠，使点A落在OC上（O为两条折痕的交点），第二条折痕与AD交于点E．请写出OC与OA的数量关系，并说明理由．
深度探究：
（3）如图3，探究小组将图1中的四边形AEA'B剪下，在AE上取中点F，将△ABF沿BF叠得到△MBF，点P，Q分别是边A'E，A'B上的动点（均不与顶点重合），将△A'PQ沿PQ折叠的对应点N恰好落在BM上，当△A'PQ的一个内角与∠A'BM相等时，请直接写出A'Q的长度．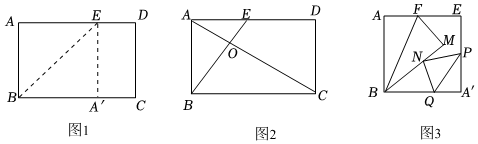
发布：2025/5/24 1:0:1组卷：724引用：3难度：0.1 -
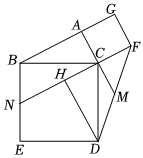3．如图，在△ABC中，∠BAC=90°，分别以AC和BC为边向外作正方形ACFG和正方形BCDE，过点D作FC的延长线的垂线，垂足为点H．连接FD，交AC的延长线于点M．下列说法：①△ABC≌△HDC；②若FG=1，DE=2，则CN=；③433=S△CFMS△CDH；④FM=DM；⑤若AG=12，tan∠ABC=3，则△FCM的面积为4．正确的个数有（ ）23发布：2025/5/24 1:0:1组卷：376引用：3难度：0.3
