综合与实践
问题情境：数学活动课上，王老师出示了一个问题：
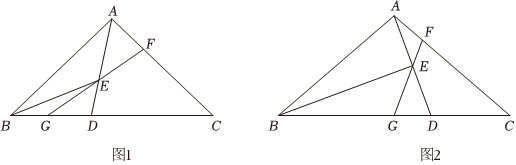
如图1，在△ABC中，AB=AC，点D是BC边上一点，连接AD，BE平分∠ABC交AD于点E，点F是AC上一点，连接FE并延长交BC于点G，∠AEF=∠ABD．求证：∠BAD=∠CGF．
独立思考：（1）请解答王老师提出的问题；
实践探究：（2）王老师提出了新问题，求证DG=AF．王老师的问题引发了同学们的思考，并积极地进行了小组讨论．在展示交流的过程中，小明同学分享了他的思路，他先发现并证明了AE和GE相等，然后又构造全等得到了结论．相信你也得到了启发，请你完成证明DG=AF；
问题解决：（3）数学活动小组同学对上述问题进行特殊化研究之后发现，如图2，当BG=CF=3AF时，可以求ADGD的值，请你尝试完成解答．
AD
GD
【考点】相似形综合题．
【答案】（1）见解析过程；
（2）见解析过程；
（3）2．
（2）见解析过程；
（3）2
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/3 0:0:1组卷：279引用：1难度：0.2
相似题
-
1．已知四边形ABCD中，E、F分别是AB、AD边上的点，DE与CF交于点G．
问题发现：
（1）①如图1，若四边形ABCD是正方形，且DE⊥CF于G，则=；DECF
②如图2，当四边形ABCD是矩形时，且DE⊥CF于G，AB=m,AD=n,则=；DECF
拓展研究：
（2）如图3，若四边形ABCD是平行四边形，且∠B+∠EGC=180°时，求证：；DECF=ADCD
解决问题：
（3）如图4，若BA=BC=5，DA=DC=10，∠BAD=90°，DE⊥CF于G，请直接写出的值．DECF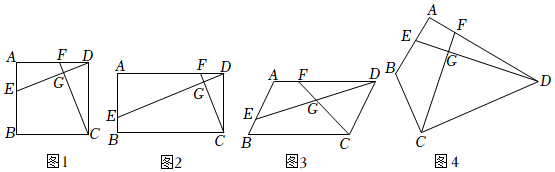
发布：2025/5/23 23:30:1组卷：2292引用：6难度：0.3 -
2．[问题情境]
（1）王老师给爱好学习的小明和小颖提出这样一个问题：如图①，在△ABC中，AB=AC，P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D，E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．
小明的证明思路是：
如图②，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE=CF．
小颖的证明思路是：
如图②，过点P作PG⊥CF，垂足为G，可以证得：PD=GF，PE=CG，则PD+PE=CF．
请你选择小明、小颖两种证明思路中的任意一种，写出详细的证明过程．
[变式探究]（2）如图③，当点P在BC延长线上时，问题情境中，其余条件不变，求证：PD-PE=CF．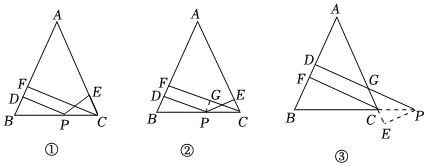
[结论运用]（3）如图④，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点C'处，点P为折痕EF上的任一点，过点P作PG⊥BE，PH⊥BG，垂足分别为G，H，若AD=8，CF=3，求PG+PH的值．
[迁移拓展]（4）图⑤是一个机器模型的截面示意图，在四边形ABCD中，E为AB边上的一点，ED⊥AD，EC⊥CB，垂足分别为D，C，且AD•CE=DE•BC，AB=2cm,AD=3cm,BD=13cm,MN分别为AE，BE的中点，连接DM，CN，请直接写出△DEM与△CEN的周长之和．37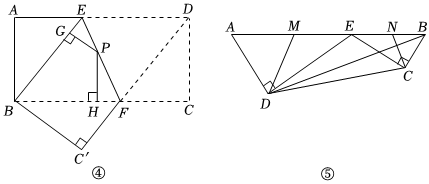
发布：2025/5/24 0:30:1组卷：278引用：1难度：0.1 -
3．在矩形ABCD中，AB=2，AD=4，F是对角线AC上不与点A，C重合的一点，过F作FE⊥AD于E，将△AEF沿EF翻折得到△GEF，点G在射线AD上，连接CG．
（1）如图1，若点A的对称点G落在AD上，∠FGC=90°，延长GF交AB于H，连接CH．
①求证：△CDG∽△GAH；
②求tan∠GHC．
（2）如图2，若点A的对称点G落在AD延长线上，∠GCF=90°，判断△GCF与△AEF是否全等，并说明理由．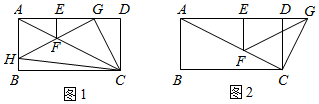
发布：2025/5/23 23:0:1组卷：1132引用：5难度：0.3
