已知椭圆E：x2a2+y2b2=1，的右焦点F（1，0），过F作直线AB交E于A，B两点，E上有两点M，N满足：MF，NF分别为∠AMB，∠ANB的角平分线．当直线AB斜率为3时，△MNF的外接圆面积为9π
（1）求E的标准方程；
（2）设直线MN：y=kx+b,求k和b的代数关系．
x
2
a
2
+
y
2
b
2
=
1
3
【考点】椭圆的准线及第二定义．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/27 0:0:1组卷：78引用：1难度：0.5
相似题
-
1．设F，E分别是椭圆
的左，右焦点，椭圆上存在点N，满足∠ENF=90°且△ENF的面积为20．x2a2+y2b2=1（a＞b＞0，a∈N*）
（1）求b的值；
（2）设点P的坐标为（1，1），直线过点P，与椭圆交于点A，B，线段AB的中点记为M．若|FM|是|FA|与|FB|的等比中项，求a的最小值，并求出此时直线l的方程．发布：2024/6/27 10:35:59组卷：99引用：1难度：0.5 -
2．已知F是椭圆5x2+9y2=45的左焦点，P是此椭圆上的动点，A（1，1）是一定点，则
的最小值为（ ）|PA|+32|PF|发布：2024/10/14 4:0:2组卷：246引用：1难度：0.5 -
3．已知椭圆C：
的左、右焦点分别为F1、F2，经过点F1且倾斜角为θx24+y23=1的直线l与椭圆交于A、B两点（其中点A在x轴上方）．将平面xOy沿x轴折叠，使y轴正半轴和x轴所确定的半平面（平面AF1F2）与y轴负半轴和x轴所确定的半平面（平面BF1F2）互相垂直．（0＜θ＜π2）
（1）若，求折叠后|AF1|+|BF1|-|AB|的值；θ=π3
（2）求折叠后的线段AB长度的取值范围，并说明理由．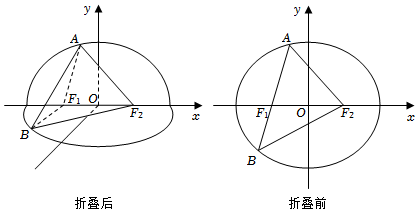
发布：2024/6/27 10:35:59组卷：174引用：3难度：0.2
