蜂房是自然界最神奇的“建筑”之一,如图1所示.蜂房结构是由正六棱柱截去三个相等的三棱锥H-ABC,J-CDE,K-EFA,再分别以AC,CE,EA为轴将△ACH,△CEJ,△EAK分别向上翻转180°,使H,J,K三点重合为点S所围成的曲顶多面体(下底面开口),如图2所示.蜂房曲顶空间的弯曲度可用曲率来刻画,定义其度量值等于蜂房顶端三个菱形的各个顶点的曲率之和,而每一顶点的曲率规定等于2π减去蜂房多面体在该点的各个面角之和(多面体的面角是多面体的面的内角,用弧度制表示).例如:正四面体在每个顶点有3个面角,每个面角是π3,所以正四面体在各顶点的曲率为2π-3×π3=π.
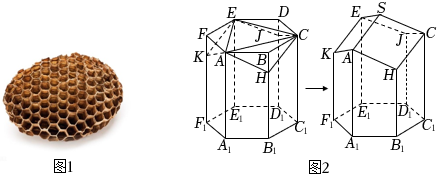
(1)求蜂房曲顶空间的弯曲度;
(2)若正六棱柱底面边长为1,侧棱长为2,设BH=x
(i)用x表示蜂房(图2右侧多面体)的表面积S(x);
(ii)当蜂房表面积最小时,求其顶点S的曲率的余弦值.
π
3
2
π
-
3
×
π
3
=
π
【考点】棱柱、棱锥、棱台的侧面积和表面积.
【答案】(1)2π;
(2)(i);
(ii).
(2)(i)
S
(
x
)
=
3
3
2
•
1
+
4
x
2
-
3
x
+
12
+
3
3
2
,
x
∈
(
0
,
2
)
(ii)
23
27
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/9 9:0:1组卷:158引用:5难度:0.4


