阅读以下材料:
斐波那契数列1,1,2,3,5,8,13,21,34,55,…
卢卡斯数列1,3,4,7,11,18,29,47,76,123,…
以上数列都有共同的特点:每一项都是整数,从第3项开始,每一项都等于前两项之和.类似的数列还有无限多个,我们称之为斐波那契一卢卡斯数列.例如:0,2,2,4,6,10,16,26,…是斐波那契一卢卡斯数列.完成以下问题:
(1)若5,a,b,33,…是斐波那契一卢卡斯数列,求2a-b的值;
(2)若1,a2,a3,a4,a5,…是斐波那契一卢卡斯数列,其中a2与a3的和大于7,且a2+a3+a4+a5<39,求a2的值.
【考点】规律型:数字的变化类.
【答案】(1)9;
(2)4.
(2)4.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/8/5 8:0:8组卷:75引用:1难度:0.5
相似题
-
1.观察以下等式:
第1个等式:;23-11×2×3=12
第2个等式:;38-12×3×4=13
第3个等式:;415-13×4×5=14
第4个等式:;524-14×5×6=15
…
按照以上规律,解决下列问题:
(1)写出第6个等式:;
(2)写出你猜想的第n(n取正整数)个等式:(用含n的等式表示),并验证等式的正确性.发布:2025/5/24 0:0:1组卷:319引用:7难度:0.7 -
2.从1到2020连续自然数的平方和12+22+32+…+20202的个位数是( )
发布:2025/5/23 23:0:1组卷:190引用:2难度:0.5 -
3.提出问题:把1到2022这2022个数,按顺时针方向依次排列在一个圆周上,从1开始按顺时针方向,保留1,擦去2,保留3,擦去4……(每隔一数;擦去一数),转圈擦下去,最后剩下的是哪个数?
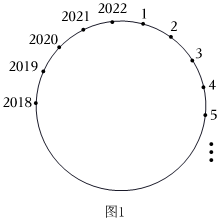
问题探究:我们先从简单情形入手,再逐次递进,最后猜想得出结论.
探究一:
如果只有1,2,很明显,留下1,擦去2,最后剩下1;
如果只有1,2,3,4,如图2所示,第一圈留下1,3擦去2,4;第二圈留下1,擦去3,最后剩下1;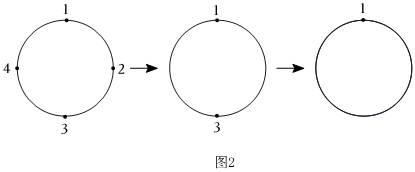
如果只有1,2,3,4,5,6,7,8,如图3所示,第一圈留下1,3,5,7擦去2,4,6,8;第二圈留下1,5擦去3,7;第三圈留下1,擦去5;最后剩下1;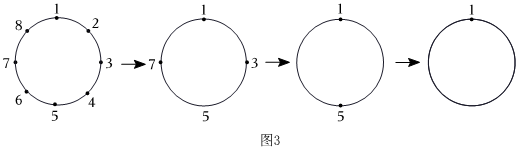
如果只有1,2,3,…,16这16个数,按顺时针方向依次排列在一个圆周上,从1开始按顺时针方向,保留1,擦去2,保留3,擦去4…(每隔一数,擦去一数),转圈擦下去,最后剩下的数是 ;
探究二:
如果只有1,2,3,4,5,6,7这7个数,由探究一可知只有4个数时,最后剩下的是1,即4个数中的“第一个数”,因此只要剩下4个数,即可知最后剩下的是哪个数.也就是先擦掉7-4=3个数,擦掉的第3个数是6,它的下一个数是7,也就是剩下的4个数中的第一个是7,所以最后剩下的数就是7;
如果只有1,2,3,…,12这12个数,由探究一可知只有8个数时,最后剩下的是1,即8个数中的“第一个数”,因此只要剩下8个数,即可知最后剩下的是哪个数.也就是先擦掉12-8=4个数,擦掉的第4个数是8,它的下一个数是9,也就是剩下的8个数中的第一个是9,所以最数学试题第7页共8页后剩下的数就是9;
仿照上面的探究方法,回答下列问题:
如果只有1,2,3,…,26这26个数,按顺时针方向依次排列在一个圆周上,从1开始按顺时针方向,保留1,擦去2,保留3,擦去4……(每隔一数,擦去一数),转圈擦下去,最后剩下的数是 ;
问题解决:
把1到2022这2022个数,按顺时针方向依次排列在一个圆周上,从1开始按顺时针方向,保留1,擦去2,保留3,擦去4……(每隔一数,擦去一数),转圈擦下去,最后剩下的数是 ;
一般规律:
把1,2,3,…,n这个数,按顺时针方向依次排列在一个圆周上,从1开始按顺时针方向,保留1,擦去2,保留3,擦去4……(每隔一数,擦去一数),转圈擦下去,如果2k<n<2k+1,且n和k都是正整数,则最后剩下的数是 ;(用n、k的代数式表示)
拓展延伸:
如果只有1,2,3,…,n这n个数,且n5000,n是正整数,按顺时针方向依次排列在一个圆周上,从1开始按顺时针方向,保留1,擦去2,保留3,擦去4…(每隔一数,擦去一数),转圈擦下去,如果最后剩下的数是2023,则n可以为 .发布:2025/5/24 0:30:1组卷:317引用:2难度:0.2


