若正三棱台ABC-A₁B₁C₁的各顶点都在表面积为65π的球O的表面上，且
AB
=
4
3
，
A
1
B
1
=
2
3
，则正三棱台ABC-A₁B₁C₁的高为（　　）

A．

B．4

C．

或3

D．3或4

【答案】D

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/5/27 14:0:0组卷：397引用：5难度：0.7

相似题

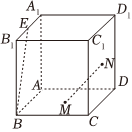1．如图，在棱长为2的正方体ABCD-A₁B₁C₁D₁中，E为棱A₁B₁的中点，M，N分别是底面ABCD与侧面CDD₁C₁的中心，P为该正方体表面上的一个动点，且满足PM⊥BE，记点P的轨迹所在的平面为α，则过N，C，B₁，C₁四点的球面被平面α截得的圆的周长是（　　）
A．
4
3
π
B．
6
5
5
π
C．
8
3
π
D．
4
5
3
π
发布：2024/12/29 12:0:2组卷：150引用：6难度：0.4
解析
2．已知一个半球内有一个内接直三棱柱ABC-A₁B₁C₁，底面ABC在半球的大圆面上，AA₁=4，BC=4
3
，∠BAC=120°，则半球的表面积为（　　）
A．64π B．72π C．80π D．96π
发布：2024/11/9 8:0:6组卷：110引用：1难度：0.7
解析
3．已知球O的直径长为12，当它的内接正四棱锥的体积最大时，该四棱锥的底面边长为（　　）
A．4 B．6 C．8 D．12
发布：2024/11/12 8:0:1组卷：24引用：0难度：0.9
解析

若正三棱台ABC-A1B1C1的各顶点都在表面积为65π的球O的表面上，且AB=43，A1B1=23，则正三棱台ABC-A1B1C1的高为（ ）