如图，抛物线y=34x2+bx+c交x轴于A，B两点，交y轴于点C，点A，B的坐标分别为（-1，0），（4，0）．
（Ⅰ）求抛物线的解析式；
（Ⅱ）点P是直线BC下方的抛物线上一动点，求△CPB的面积最大时点P的坐标；
（Ⅲ）若M是抛物线上一点，且∠MCB=∠ABC，请直接写出点M的坐标．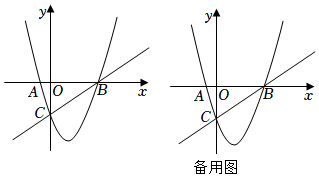
3
4
【考点】二次函数综合题．
【答案】（Ⅰ）y=；（Ⅱ）（2，-）；（Ⅲ）（3，-3）或（，）．
3
4
x
2
-
9
4
x
-
3
9
2
53
7
1125
49
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/4 1:0:1组卷：884引用：4难度：0.3
相似题
-
1．如图1，抛物线y=ax2+bx+4与x轴交于A，B两点，与y轴交于点C，AB=8，B点横坐标为2，延长矩形OBDC的DC边交抛物线于E．
（1）求抛物线的解析式；
（2）如图2，若点P是直线EO上方的抛物线上的一个动点，过点P作x轴的垂线交直线EO于点M，求PM的最大值；
（3）如图3，如果点F是抛物线对称轴l上一点，抛物线上是否存在点G，使得以F，G，A，C为顶点的四边形是平行四边形？若存在，求出所有满足条件的点G的坐标；若不存在，请说明理由．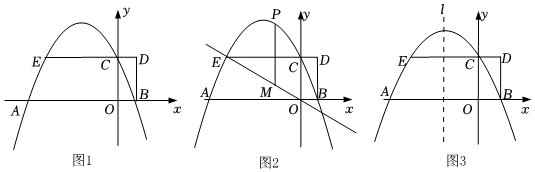
发布：2025/6/7 7:0:1组卷：565引用：8难度：0.1 -
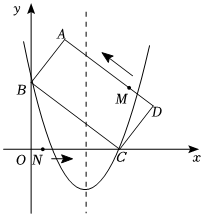2．如图，在平面直角坐标系中，矩形ABCD的边BC与x轴、y轴的交点分别为C（8，0），B（0，6），CD=5，抛物线y=ax2-x+c（a≠0）过B，C两点，动点M从点D开始以每秒5个单位长度的速度沿D→A→B→C的方向运动到达C点后停止运动．动点N从点O以每秒4个单位长度的速度沿OC方向运动，到达C点后，立即返回，向CO方向运动，到达O点后，又立即返回，依此在线段OC上反复运动，当点M停止运动时，点N也停止运动，设运动时间为t.154
（1）求抛物线的解析式；
（2）求点D的坐标；
（3）当点M，N同时开始运动时，若以点M，D，C为顶点的三角形与以点B，O，N为顶点的三角形相似，直接写出t的值．发布：2025/6/7 16:30:2组卷：39引用：2难度：0.1 -
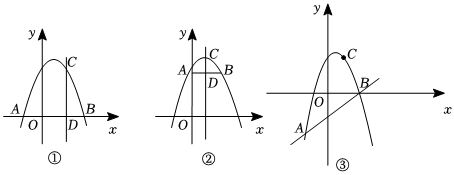
3．在平面直角坐标系中，直线AB与抛物线y=ax2+bx+c交于A，B（点A在点B的左侧）两点，点C是该抛物线上任意一点，过C点作平行于y轴的直线交AB于D，分别过点A，B作直线CD的垂线，垂足分别为点E，F．
特例感悟：
（1）已知：a=-2，b=4，c=6．
①如图①，当点C的横坐标为2，直线AB与x轴重合时，CD=，|a|•AE•BF=．
②如图②，当点C的横坐标为1，直线AB∥x轴且过抛物线与y轴的交点时，CD=，|a|•AE•BF=．
③如图③，当点C的横坐标为2，直线AB的解析式为y=x-3时，CD=，|a|•AE•BF=．
猜想论证：
（2）由（1）中三种情况的结果，请你猜想在一般情况下CD与|a|•AE•BF之间的数量关系，并证明你的猜想．拓展应用．
（3）若a=-1，点A，B的横坐标分别为-4，2，点C在直线AB的上方的抛物线上运动（点C不与点A，B重合），在点C的运动过程中，利用（2）中的结论求出△ACB的最大面积．发布：2025/6/7 7:0:1组卷：21引用：2难度：0.3
