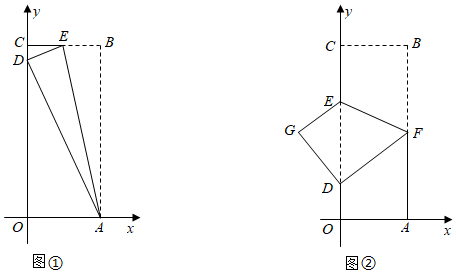
将一个矩形纸片OABC放置在平面直角坐标系中，OA，OC分别在x轴，y轴的正半轴上，点B坐标为（4，10）．
（Ⅰ）如图①，将矩形纸片OABC折叠，使点B落在y轴上的点D处，折痕为线段AE，求点D坐标；
（Ⅱ）如图②，点E，F分别在OC，AB边上．将矩形纸片OABC沿线段EF折叠，使得点B与点D（0，2）重合，求点C的对应点G的坐标；
（Ⅲ）在（Ⅱ）的条件下，若点P是坐标系内任意一点，点Q在y轴上，使以点D，F，P，Q为顶点的四边形是菱形，请直接写出满足条件的点P的坐标．
【考点】四边形综合题．
【答案】（Ⅰ）点D的坐标为（0，2 ）；
（Ⅱ）点G的坐标为（-，）；
（Ⅲ）点P的坐标为（4，10），（4，0），（-4，5），（4，）．
21
（Ⅱ）点G的坐标为（-
12
5
26
5
（Ⅲ）点P的坐标为（4，10），（4，0），（-4，5），（4，
5
6
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/17 8:0:9组卷：2277引用：10难度：0.4
相似题
-
1．如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，
AE平分∠DAM．
（1）写出AM、AD、MC三条线段的数量关系：；
请对你猜想的结论进行证明；
（2）写出AM、DE、BM三条线段的数量关系：.（不必证明）
拓展延伸：
若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，（1）、（2）中的结论是否成立？请分别作出判断，不需要证明．
发布：2025/5/21 19:0:1组卷：44引用：4难度：0.3 -
2．【基础问题】
如图①，矩形ABCD中，点E为AB边上一点，连接DE，作EF⊥DE交BC于点F，且DE=FE，求证：△AED≌△BFE．
【拓展延伸】
（1）如图②，点E为平行四边形ABCD内部一点，EA=EB，DA⊥AE，作DF⊥BA交BA延长线于点F，若DA=2EA，AB=5，则平行四边形ABCD的面积为 ；
（2）如图③，在正方形ABCD中，AD=6，在CD边上取一点E，使EC=2DE，将△AED沿AE翻折到△AED′位置，作D′F⊥AB于点F，在D′F右侧作∠FGD'=90°，则△FGD'面积的最大值为 ．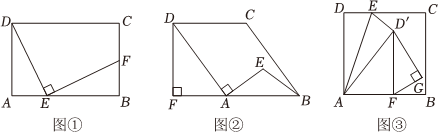
发布：2025/5/21 17:0:2组卷：160引用：1难度：0.3 -
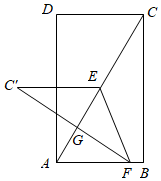3．如图，矩形ABCD中，AB=2，BC=4，连结对角线AC，E为AC的中点，F为AB边上的动点，连结EF，作点C关于EF的对称点C′，连结C′E，C′F，若△EFC′与△ACF的重叠部分（△EFG）面积等于△ACF的3，则BF=．14发布：2025/5/21 18:0:1组卷：1667引用：8难度：0.1
