如图，△ABD内接于半径为5的⊙O，连接AO并延长交BD于点M，交⊙O于点过点A作AE∥BD，交CD的延长线于点E，AB=AM．
（1）求证：△ABM∽△ECA．
（2）当CM=4OM时，求AD的长；
（3）当CM=k•OM时，设△MCD的面积为S1，△ADE的面积为S2，求s1s2的值．（用含k的代数式表示）．
s
1
s
2
【考点】圆的综合题．
【答案】（1）证明见解答过程；
（2）AD=4；
（3）．
（2）AD=4
5
（3）
k
2
2
k
2
+
6
k
+
4
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/21 8:0:9组卷：113引用：1难度：0.2
相似题
-
1．[问题提出]
（1）如图1，已知线段AB=4，点C是一个动点，且点C到点B的距离为2，则线段AC长度的最大值是 ；
[问题探究]
（2）如图2，以正方形ABCD的边CD为直径作半圆O，E为半圆O上一动点，若正方形的边长为2，求AE长度的最大值；
[问题解决]
（3）如图3，某植物园有一块三角形花地ABC，经测量，AC=20米，BC=120米，∠ACB=30°，BC下方有一块空地（空地足够大），为了增加绿化面积，管理员计划在BC下方找一点P，将该花地扩建为四边形ABPC，扩建后沿AP修一条小路，以便游客观赏．考虑植物园的整体布局，扩建部分△BPC需满足∠BPC=60°．为容纳更多游客，要求小路AP的长度尽可能长，问修建的观赏小路AP的长度是否存在最大值？若存在，求出AP的最大长度；若不存在，请说明理由．3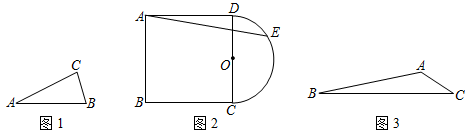
发布：2025/5/23 10:30:1组卷：904引用：8难度：0.2 -
2．问题研究．
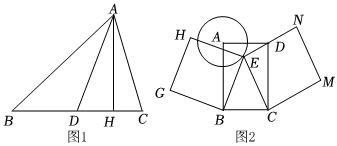
如图1，AD是△ABC的中线，AH是BC边上的高．
（1）当AH=6，CD=5，DH=3时，AB=．
（2）求证：AB2+AC2=2AD2+2BD2．
问题解决
（3）某地为打造元宵节灯展景观，需按如下要求设计一批灯展造型．如图2，矩形ABCD是造型框架，以顶点A为圆心悬挂圆形灯架（⊙A），以B，C为顶点钉两个正方形展板（正方形BEHG和正方形CENM），接合点点E恰好在⊙A上．若AD=1.4m,AB=2.4m,⊙A的半径为0.7m,求两个正方形展板面积和的最小值．发布：2025/5/23 10:30:1组卷：128引用：3难度：0.1 -
3．如图，已知O是△ABC边AB上的一点，以O为圆心、OB为半径的⊙O与边AC相切于点D，且BC=CD，连接OC，交⊙O于点E，连接BE并延长，交AC于点F．
（1）求证：BC是⊙O切线；
（2）求证：OA•AB=AD•AC；
（3）若，求EO的长．AC=10，tan∠BAC=43发布：2025/5/23 11:30:2组卷：738引用：4难度：0.3
