观察下面三行数：
第一行：2，-4，8，-16，32，-64，…；
第二行：5，-1，11，-13，35，-61，…；
第三行：-1，2，-4，8，-16，32…．
（1）第一行的第7个数是
128
128
；
（2）第二、三行数与第一行数分别有什么关系？
（3）取每行数的第8个数，计算这三个数的和．

【答案】128

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/8/23 6:0:3组卷：55引用：3难度：0.5

相似题

1．观察下列等式：
①
3
2
-
1
2
4
=
1
+
1
；
②
4
2
-
2
2
4
=
1
+
2
；
③
5
2
-
3
2
4
=
1
+
3
；
④
6
2
-
4
2
4
=
1
+
4
；
⑤
7
2
-
5
2
4
=
1
+
5
；
…
（1）请按以上规律写出第⑥个等式
；
（2）猜想并写出第n个等式
；并证明猜想的正确性．
（3）利用上述规律，计算：
3
2
-
1
2
-
4
4
+
4
2
-
2
2
-
4
4
+
5
2
-
3
2
-
4
4
+
…
+
2021
2
-
2019
2
-
4
4
=
．
发布：2025/6/9 22:30:2组卷：254引用：4难度：0.4
解析
2．古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”，而把1、4、9、16　…这样的数称为“正方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和，下列等式中符合这一规律的是（　　）
A．13=3+10 B．25=9+16 C．36=14+22 D．49=21+28
发布：2025/6/9 21:30:1组卷：160引用：4难度：0.6
解析
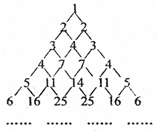3．如图的数表，它有这样的规律：表中第1行为1，第n （n≥2）行两端的数均为n,其余每一个数都等于它肩上两个数的和，设第n （n≥2）行的第2个数为a_n，如a₂=2，a₃=4，则a_n+1-a_n=

（n≥2），a_n=

．
发布：2025/6/9 20:0:1组卷：124引用：2难度：0.7
解析

3．如图的数表，它有这样的规律：表中第1行为1，第n （n≥2）行两端的数均为n,其余每一个数都等于它肩上两个数的和，设第n （n≥2）行的第2个数为an，如a2=2，a3=4，则an+1-an= （n≥2），an= ．