如图，直角三角形ACB，直角顶点C在直线l上，分别过点A、B作直线l的垂线，垂足分别为点D和点E．

（1）求证：∠DAC=∠BCE；
（2）如果AC=BC．
①求证：CD=BE；
②若设△ADC的三边分别为a、b、c,试用此图证明勾股定理．

【答案】（1）证明过程见解答；
（2）①证明过程见解答；
②证明过程见解答．

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/8/12 0:0:0组卷：1516引用：9难度：0.6

相似题

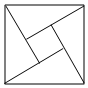1．如图，“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼接成的大正方形，若直角三角形的两条直角边长分别为a,b（a＞b），大正方形的面积为S₁，小正方形的面积为S₂，则用含S₁，S₂的代数式表示（a+b）²正确的是（　　）
A．S₁ B．S₂ C．2S₁-S₂ D．2S₂-S₁
发布：2025/5/26 4:0:1组卷：982引用：7难度：0.5
解析
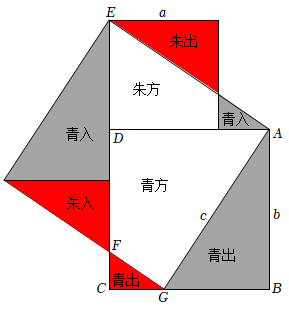
2．我国是最早了解勾股定理的国家之一，东汉末年数学家刘徽在为《九章算术》作注中依据割补术而创造了勾股定理的无字证明“青朱出入图”，移动几个图形就直观地证明了勾股定理，如图，若a=3，b=4，则△CFG的面积为
．
发布：2025/5/26 4:0:1组卷：110引用：1难度：0.6
解析
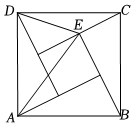3．汉代数学家赵爽为了证明勾股定理，构造了一副“弦图”，后人称其为“赵爽弦图”．如图，大正方形ABCD由四个全等的直角三角形和一个小正方形组成，若∠ADE=∠AED，
AD
=
2
5
，则△ADE的面积为（　　）
A．6 B．5 C．
2
5
D．
2
10
发布：2025/5/25 11:30:2组卷：357引用：3难度：0.5
解析

如图，直角三角形ACB，直角顶点C在直线l上，分别过点A、B作直线l的垂线，垂足分别为点D和点E．（1）求证：∠DAC=∠BCE；（2）如果AC=BC．①求证：CD=BE；②若设△ADC的三边分别为a、b、c,试用此图证明勾股定理．