如图，已知正方形ABCD的边长为8个单位长，点E为AD边上的中点，点P从点A向点B以1个单位长/秒速度匀速运动，连接PE，过点P作PE的垂线，交BC于点F．交射线DC于点G．设点P运动时间为t.
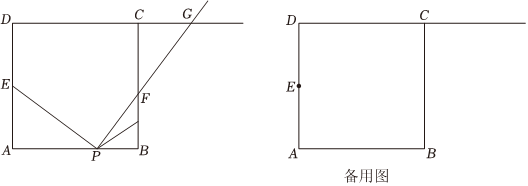
（1）用含t的代数式表示BF长为 -t24+2t-t24+2t；
（2）如图，点K在BC边上，且BK=2，求点K在∠EPG内部（包括边上）的时长；
（3）①求证：点P一定在△DEG的外接圆上；
②当△DEG的外接圆与AB相切时，求t的值；
（4）线段CG长的最小值是 82-882-8．
-
t
2
4
-
t
2
4
2
2
【考点】圆的综合题．
【答案】+2t；8-8
-
t
2
4
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/18 8:0:8组卷：104引用：2难度：0.3
相似题
-
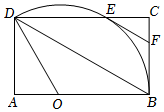1．如图，点O是矩形ABCD中AB边上的一点，以O为圆心，OB为半径作圆，⊙O交CD边于点E，且恰好过点D，连接BD，过点E作EF∥BD．
（1）若∠BOD=120°，
①求∠CEF的度数；
②求证：EF是⊙O的切线．
（2）若CF=2，FB=3，求OD的长．发布：2025/5/25 13:0:1组卷：301引用：3难度：0.4 -
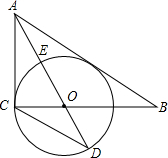2．如图，在Rt△ABC中，∠ACB=90°，AO是△ABC的角平分线．以O为圆心，OC为半径作⊙O．
（1）求证：AB是⊙O的切线．
（2）已知AO交⊙O于点E，延长AO交⊙O于点D，tanD=，求12的值．AEAC
（3）在（2）的条件下，设⊙O的半径为3，求AB的长．发布：2025/5/25 13:30:1组卷：5031引用：18难度：0.1 -
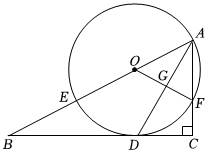3．如图，在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于点D，O为AB上一点，经过点A，D的⊙O分别交AB，AC于点E、F，连接OF交AD于点G．
（1）求证：BC是⊙O的切线；
（2）求证：AD2=AB•AF；
（3）若BE=8，tanB=，求AD的长．512发布：2025/5/25 14:0:1组卷：308引用：1难度：0.3
