问题：阅读下面材料，解决后面的问题：
我们知道，三角形的面积等于二分之一底乘高．在学习了三角函数后，还可以这样求三角形的面积：对△ABC，a,b,c分别为∠A，∠B，∠C的对边，则其面积
S=12absinC
=12bcsinA
=12casinB
（1）在△ABC中，∠A=30°，b=2，c=3，求b边对应的高的长度．
（2）如图2，在△ABC中，已知AB=2，BC=1，D为AC上一点，证明：BD=2sin（∠1+∠2）2sin∠1+sin∠2．
（3）正数a,b,c,d,e,f满足a+b=c+d=e+f=1，证明：af+bc+de＜1．
S
=
1
2
absin
C
1
2
bcsin
A
1
2
casin
B
BD
=
2
sin
（
∠
1
+
∠
2
）
2
sin
∠
1
+
sin
∠
2
【考点】几何变换综合题．
【答案】（1）；
（2）证明过程详见解答；
（3）证明过程详见解答．
3
2
（2）证明过程详见解答；
（3）证明过程详见解答．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/13 8:0:9组卷：89引用：1难度：0.1
相似题
-
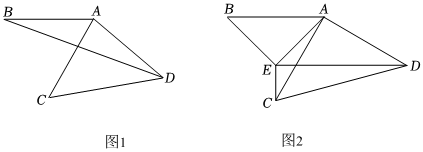
1．将线段AB绕点A逆时针旋转60°得到线段AC，继续旋转α（0°＜α＜120°）得到线段AD，连接CD．
（1）连接BD，
①如图1，若α=80°，则∠BDC的度数为 ；
②在第二次旋转过程中，请探究∠BDC的大小是否改变．若不变，求出∠BDC的度数；若改变，请说明理由．
（2）如图2，以AB为斜边作直角三角形ABE，使得∠B=∠ACD，连接CE，DE．若∠CED=90°，求α的值．发布：2025/6/23 16:0:1组卷：633引用：8难度：0.1 -
2．如图，△ABC为边长是4
的等边三角形，四边形DEFG是边长是6的正方形．现将等边△ABC和正方形DEFG按如图①的方式摆放，使点C与点E重合，点B、C、E、F在同一条直线上，△ABC从图①的位置出发，以每秒1个单位长度的速度沿EF方向向右匀速运动，当点B与点E重合时停止运动，设△ABC的运动时间为t秒．3
（1）当点A与点D重合时，求此时t的值；
（2）在整个运动过程中，设等边△ABC和正方形DEFG重叠部分的面积为S，求S与t之间的函数关系式；
（3）如图②，当点A与点D重合时，作∠ABE的角平分线BM交AE于点M，将△ABM绕点A逆时针旋转，使边AB与边AC重合，得到△ACN．在线段AG上是否存在H点，使得△ANH为等腰三角形？若存在，求线段AH的长度；若不存在，请说明理由．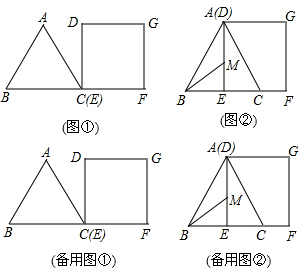
发布：2025/6/24 11:30:1组卷：111引用：1难度：0.3 -
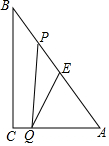3．如图，Rt△ABC中，∠C=90°，BC=8cm,AC=6cm.点P从 B出发沿BA向A运动，速度为每秒1cm,点E是点B以P为对称中心的对称点，点P运动的同时，点Q从A出发沿AC向C运动，速度为每秒2cm,当 点Q到达顶点C时，P，Q同时停止运动，设P，Q两点运动时间为t秒．
（1）当t为何值时，PQ∥BC？
（2）设四边形PQCB的面积为y,求y关于t的函数关系式；并说明四边形PQCB面积能否是△ABC面积的？若能，求出此时t的值；若不能，请说明理由；35
（3）当t为何值时，△AEQ为等腰三角形？发布：2025/6/23 11:30:2组卷：267引用：3难度：0.3
