已知双曲线T：x2a2-y2b2=1实轴AB长为4（A在B的左侧），双曲线Γ上第一象限内的一点P到两渐近线的距离之积为45．
（1）求双曲线Γ的标准方程；
（2）设过T（4，0）的直线与双曲线交于C，D两点，记直线AC，BD的斜率为k1，k2，请从下列的结论中选择一个正确的结论，并予以证明．
①k1+k2为定值；②k1•k2为定值；③k1k2为定值．
x
2
a
2
-
y
2
b
2
4
5
k
1
k
2
【答案】（1）．
（2）③为正确结论．
x
2
4
-
y
2
=
1
（2）③为正确结论．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/28 8:0:9组卷：91引用：1难度：0.2
相似题
-
1．已知双曲线C：
=1（a＞0，b＞0）的左顶点为A，过左焦点F的直线与C交于P，Q两点．当PQ⊥x轴时，|PA|=x2a2-y2b2，△PAQ的面积为3．10
（1）求C的方程；
（2）证明：以PQ为直径的圆经过定点．发布：2024/12/18 0:0:1组卷：707引用：8难度：0.5 -
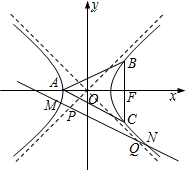2．如图，在平面直角坐标系xOy中，已知等轴双曲线E：（a＞0，b＞0）的左顶点A，过右焦点F且垂直于x轴的直线与E交于B，C两点，若△ABC的面积为x2a2-y2b2=1．2+1
（1）求双曲线E的方程；
（2）若直线l：y=kx-1与双曲线E的左，右两支分别交于M，N两点，与双曲线E的两条渐近线分别交于P，Q两点，求的取值范围．|MN||PQ|发布：2024/10/31 12:30:1组卷：541引用：11难度：0.5 -
3．已知双曲线
的左、右焦点分别为F1，F2，过F1的直线与C的两条渐近线分别交于A，B两点，若A为线段BF1的中点，且BF1⊥BF2，则C的离心率为（ ）C：x2a2-y2b2=1（a＞0，b＞0）发布：2024/11/8 21:0:2组卷：445引用：8难度：0.5
