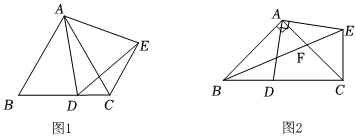
在△ABC中，AB=AC，D是边BC上一点，点E在AD的右侧，线段AE=AD，且∠DAE=∠BAC=α．
（1）如图1，若α=60°，连接CE，DE．则∠ADE的度数为 60°60°；BD与CE的数量关系是 BD=CEBD=CE．
（2）如图2，若α=90°，连接EC、BE．试判断△BCE的形状，并说明理由．
【考点】全等三角形的判定与性质．
【答案】60°；BD=CE
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/5 18:0:8组卷：3476引用：11难度：0.3
相似题
-
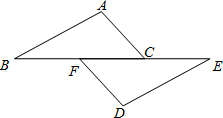1．如图，已知：点B、F、C、E在一条直线上，FB=CE，AC=DF．能否由上面的已知条件证明AB∥ED？如果能，请给出证明；如果不能，请从下列三个条件中选择一个合适的条件，添加到已知条件中，使AB∥ED成立，并给出证明．供选择的三个条件（请从其中选择一个）：
①AB=ED；
②BC=EF；
③∠ACB=∠DFE．发布：2025/6/18 2:30:1组卷：279引用：41难度：0.5 -
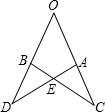
2．如图，OA=OB，OC=OD，∠O=50°，∠D=35°，则∠AEC=．
发布：2025/6/18 2:30:1组卷：694引用：18难度：0.9 -
3．（1）已知：如图①，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=60°．
求证：①AC=BD；
②∠APB=60°．
（2）如图②，在△AOB和△COD中，若OA=OB，OC=OD，∠AOB=∠COD=α，则AC与BD间的等量关系式为；∠APB的大小为．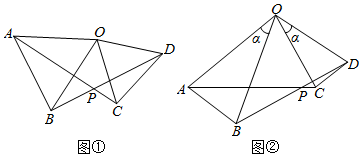
发布：2025/6/18 1:30:1组卷：211引用：3难度：0.6
