如图1，在半径为2的扇形AOB中，∠AOB=90°，点C是AB上的一个动点（不与点A、B重合），点F是BC的中点，OF交BC于D，OE⊥AC于E．
（1）当BC=2时，求线段OD的长；
（2）在△DOE中是否存在长度保持不变的边？如果存在，请指出并求其长度，如果不存在，请说明理由．
（3）设BD=x,S△DOE=y,求y关于x的函数关系式，并写出自变量取值范围．
【考点】圆的综合题．
【答案】（1）；
（2）在△DOE中是存在长度保持不变的边，DE=；
（3）y=（0＜x）．
3
（2）在△DOE中是存在长度保持不变的边，DE=
2
（3）y=
4
-
x
2
+
x
4
-
x
2
4
＜
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/21 2:0:8组卷：113引用：1难度：0.2
相似题
-
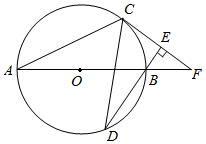1．如图，AB为⊙O的直径，C，D为⊙O上不同于A，B的两点，∠ABD=2∠BAC，连接CD．过点C作CE⊥DB，垂足为E，直线AB与CE相交于点F．
（1）求证：CF为⊙O的切线；
（2）求证：AB•BF=2BE•OF；
（3）当BF=5，sinF=时，求BD的长．35发布：2025/5/25 17:0:1组卷：269引用：1难度：0.1 -
2．如图，在Rt△ABC中，∠ABC=90°，O是AB边上一点，以O为圆心，OA长为半径的圆分别交AB，AC于点D，E，点F是AB边延长线上一点，连接EF交BC边于点G，且GE=GC．
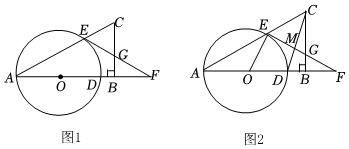
（1）求证：EF是⊙O的切线；
（2）若AE=EF，求∠A的度数；
（3）如图2，在（2）的条件下，连接CD交线段EF于点M．若BD=BF，求的值．MDMC发布：2025/5/25 17:30:1组卷：315引用：1难度：0.3 -
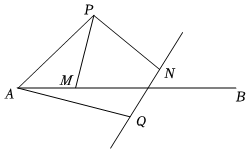3．如图，点P在射线AB的上方，0°＜∠PAM＜60°、PA=4，点M是射线AB上的动点（点M不与点A重合），现将点P绕点A按顺时针方向旋转60°到点Q，将点M绕点P按逆时针方向旋转60°到点N，连接AQ，PM，PN，作直线QN．
（1）求证：AM=QN；
（2）直线QN与以点P为圆心，PN的长为半径的圆是否存在相切的情况？若存在，请求出此时∠APN和∠PAM的关系，若不存在，请说明理由；
（3）若∠PAB=50°，当以点P为圆心，PN长为半径的圆经过点Q时，直接写出劣弧NQ与两条半径所围成的扇形的面积．发布：2025/5/25 17:30:1组卷：45引用：1难度：0.4
