折纸,操作简单,富有数学趣味,常常能为证明一个命题提供思路和方法.
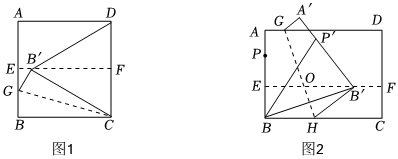
【动手操作】如图1,把正方形纸片ABCD对折后再展开,折痕为EF;将点B翻折到EF上点B′,折痕为CG;连接B′D.
(1)判断△B′CD的形状并说明理由;
【类比操作】如图2,点P为长方形纸片ABCD的边AB上一点,折叠纸片,使B与P两点重合,展平纸片,得到折痕EF;折叠纸片,使点B折叠后落在EF上的点B处,展平纸片,得到折痕GH、EF与GH交于点O;连接BP′、BB′.
(2)求证:点O在BP′的垂直平分线上;
(3)试探究∠P′BB′与∠CBB′之间的数量关系,并说明理由.
【考点】四边形综合题.
【答案】(1)△B′CD是等边三角形,理由见解答;
(2)证明过程见解答;
(3)∠P′BB′=2∠CBB′,理由见解答.
(2)证明过程见解答;
(3)∠P′BB′=2∠CBB′,理由见解答.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/7 6:0:2组卷:208引用:1难度:0.1
相似题
-
1.如图1,在正方形ABCD中,点E是BC边上的一点,∠AEP=90°,且EP交正方形外角的平分线CP于点P.
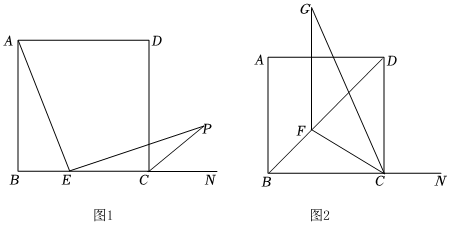
(1)求∠ECP的度数;
(2)求证:AE=EP;
(3)在AB边上是否存在点M,使得四边形DEPM是平行四边形?若存在,请画出图形并给予证明;若不存在,请说明理由;
(4)如图2,在边长为4的正方形ABCD中,将线段AB沿射线BD平移,得到线段GF,连接CG、CF则直接写出CF+CG的最小值是 .发布:2025/6/8 3:30:1组卷:41引用:1难度:0.2 -
2.已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.

(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中,已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.发布:2025/6/8 5:0:1组卷:859引用:16难度:0.1 -
3.在平面直角坐标系xOy中,已知,点A(a,0),M(b,a),其中a,b满足
,9-3b=12a-a2-36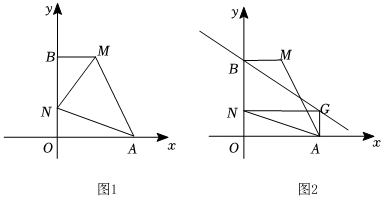
(1)请直接写出a,b的值;
(2)如图1,过点M作MB⊥y轴于点B,N为y轴上一点,且∠MAN=45°,求点N的坐标;
(3)如图2,在(2)的条件下,已知G为第一象限内一点,∠AGN=90°,当OG的值最大时,
①判断四边形OAGN的形状(不必并说明理由);
②P是y轴上一点,在直线BG上是否存在点Q,使以B,M,P,Q为顶点的四边形为平行四边形?若存在,请求出点Q及对应的点P的坐标;若不存在,请说明理由.发布:2025/6/8 4:0:1组卷:121引用:3难度:0.1


